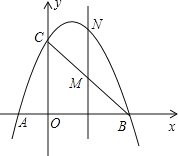
【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N若点M的横坐标为m,请用m的代数式表示MN的长。
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由。
参考答案:
【答案】(1)y=﹣x2+2x+3.(2) ﹣m2+3m(0<m<3).(3) 当m=![]() 时,△BNC的面积最大,最大值为
时,△BNC的面积最大,最大值为![]() .
.
【解析】试题分析:(1)利用待定系数法求二次函数的解析式;
(2)先求直线BC的解析式,表示出M、N两点的坐标,利用纵坐标的差计算MN的长即可;
(3)根据面积公式得:S△BNC=S△CMN+S△MNB=![]() |MN||OB|,OB的长是定值为3,所以MN的最大值即为面积的最大值,求MN所表示的二次函数的最值即可.
|MN||OB|,OB的长是定值为3,所以MN的最大值即为面积的最大值,求MN所表示的二次函数的最值即可.
解:(1) ∵抛物线经过点A(1,0),B(3,0),C(0,3)三点,
∴设抛物线的解析式为:y=a(x+1)(x3),
把C(0,3)代入得:3=a(0+1)(03),
a=1,
∴抛物线的解析式:y=-x2+2x+3
(2) 设直线BC的解析式为:y=kx+b,
把B(3,0),C(0,3)代入得: ![]() ,
,
解得:
![]() ,
,
∴直线BC的解析式为y=-x+3,
∴M(m,-m+3),
又∵MN⊥x轴,
∴N(m,-m2+2m+3),
∴MN=(-m2+2m+3)-(-m+3)=-m2+3m(0<m<3)
(3)S△BNC=S△CMN+S△MNB=![]() |MN|·|OB|,
|MN|·|OB|,
∴当|MN|最大时,△BNC的面积最大,
MN=-m2+3m=-(m-![]() )2+
)2+![]() ,
,
所以当m=![]() 时,△BNC的面积最大为
时,△BNC的面积最大为![]() ×
×![]() ×3=
×3=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.

(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式?
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】金瑞公司决定从厂家购进甲、乙两种不同型号的显示器共50台,购进显示器的总金额不超过77000元,已知甲、乙型号的显示器价格分别为1000元/台、2000元/台.
(1)求金瑞公司至少购进甲型显示器多少台?
(2)若甲型显示器的台数不超过乙型显示器的台数,则有哪些购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王从A地前往B地,到达后立刻返回.他与A地的距离y(千米)和所用时间x(小时)之间的函数关系如图所示.
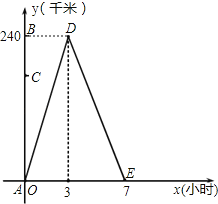
(1)小王从B地返回到A地用了多少小时?
(2)求小王出发6小时后距A地多远?
(3)在A、B之间有一C地,小王从去吋途经C地,到返回时路过C地,共用了2小时20分,求A、C 两地相距多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在促销期间规定:商场内所有商品按标价的80%出售,同时当顾客在该商场消费满一定金额后,按如下方案获得相应金额的奖券:
消费金额a(元)范围
200≤a<400
400≤a<500
500≤a<700
700≤a<900
…
获得奖券的金额(元)
30
60
100
130
…
根据上述促销方法,顾客在商场内购物可以获得双重优惠。例如,购买标价为450元的商品,则消费金额为
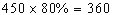 元,获得的优惠额为450×(1-80%)+30=120元,设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价。
元,获得的优惠额为450×(1-80%)+30=120元,设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价。(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在500元与800元之间(含500元和800元)的商品,顾客购买标价为多少元的商品,可以得到
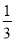 的优惠率?
的优惠率? -
科目: 来源: 题型:
查看答案和解析>>【题目】你一定知道乌鸦喝水的故事吧!一个紧口瓶中盛有一些水,乌鸦想喝,但是嘴够不着瓶中的水,于是乌鸦衔来一些小石子放入瓶中,瓶中水面的高度随石子的增多而上升,乌鸦喝到了水.但是还没解渴,瓶中水面就下降到乌鸦够不着的高度,乌鸦只好再去衔些石子放入瓶中,水面又上升,乌鸦终于喝足了水,哇哇地飞走了.如果设衔入瓶中石子的体积为x,瓶中水面的高度为Y,下面能大致表示上面故事情节的图象是( )
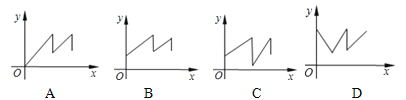
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
相关试题

