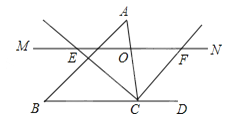
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?
并说明理由.
参考答案:
【答案】(1)证明见解析;(2)5;(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.证明见解析.
【解析】试题分析:(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案;(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可得出CO的长;(3)根据平行四边形的判定以及矩形的判定得出即可.
试题解析:(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF=![]() =10,
=10,
∴OC=![]() EF=5;
EF=5;
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=3x2先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( )
A.y=3(x+1)2+1
B.y=3(x+1)2﹣1
C.y=3(x﹣1)2+1
D.y=3(x﹣1)2﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果5akb与-4a2b是同类项,那么5akb+(-4a2b)=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④当AD=4时,△DEF的面积的最小值为
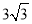 .其中结论正确的个数是( )
.其中结论正确的个数是( )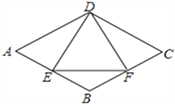
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中正确的是( )
A.b3b2=b6B.x3+x3=x6C.a2÷a2=0D.(﹣a3)2=a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正多边形的外角为72°,则这个正多边形的内角和为( )
A.360°B.540°C.720°D.900°
-
科目: 来源: 题型:
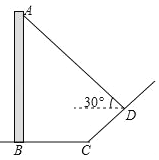
查看答案和解析>>【题目】(2016山东潍坊第22题)如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
相关试题

