【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
参考答案:
【答案】
(1)
解: ∵四边形ABCO为矩形,
∴∠OAB=∠AOC=∠B=90°,AB=CO=8,AO=BC=10.
由题意,△BDC≌△EDC.
∴∠B=∠DEC=90°,EC=BC=10,ED=BD.
由勾股定理易得EO=6.
∴AE=10﹣6=4,
设AD=x,则BD=ED=8﹣x,由勾股定理,得x2+42=(8﹣x)2,
解得,x=3,∴AD=3.
∵抛物线y=ax2+bx+c过点D(3,10),C(8,0),O(0,0)
∴ ![]() ,
,
解得 
∴抛物线的解析式为:y=﹣ ![]() x2+
x2+ ![]() x.
x.
(2)
解:方法一:
∵∠DEA+∠OEC=90°,∠OCE+∠OEC=90°,
∴∠DEA=∠OCE,
由(1)可得AD=3,AE=4,DE=5.
而CQ=t,EP=2t,∴PC=10﹣2t.
当∠PQC=∠DAE=90°,△ADE∽△QPC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t= ![]() .
.
当∠QPC=∠DAE=90°,△ADE∽△PQC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t= ![]() .
.
∴当t= ![]() 或
或 ![]() 时,以P、Q、C为顶点的三角形与△ADE相似.
时,以P、Q、C为顶点的三角形与△ADE相似.
方法二:
∵E(0,6),C(8,0),
∴lEC:y=﹣ ![]() x+6,
x+6,
∵ ![]() ,EP=2t,
,EP=2t,
∴Px= ![]() t,
t,
∴P( ![]() t,﹣
t,﹣ ![]() t+6),Q(8﹣t,0),
t+6),Q(8﹣t,0),
∵△PQC∽△ADE,且∠ECO=∠AED,
∴PQ⊥OC或PQ⊥PC.
当PQ⊥OC时,Px=Qx,即 ![]() t=8﹣t,∴t1=
t=8﹣t,∴t1= ![]() ,
,
当PQ⊥PC时,KPQKPC=﹣1,∴t2= ![]() .
.
(3)
解:方法一
假设存在符合条件的M、N点,分两种情况讨论:
① 
EC为平行四边形的对角线,由于抛物线的对称轴经过EC中点,若四边形MENC是平行四边形,那么M点必为抛物线顶点;
则:M(4, ![]() );而平行四边形的对角线互相平分,那么线段MN必被EC中点(4,3)平分,则N(4,﹣
);而平行四边形的对角线互相平分,那么线段MN必被EC中点(4,3)平分,则N(4,﹣ ![]() );
);
②EC为平行四边形的边,则EC ![]() MN,设N(4,m),则M(4﹣8,m+6)或M(4+8,m﹣6);
MN,设N(4,m),则M(4﹣8,m+6)或M(4+8,m﹣6);
将M(﹣4,m+6)代入抛物线的解析式中,得:m=﹣38,此时 N(4,﹣38)、M(﹣4,﹣32);
将M(12,m﹣6)代入抛物线的解析式中,得:m=﹣26,此时 N(4,﹣26)、M(12,﹣32);
综上,存在符合条件的M、N点,且它们的坐标为:
①M1(﹣4,﹣32),N1(4,﹣38);②M2(12,﹣32),N2(4,﹣26);③M3(4, ![]() ),N3(4,﹣
),N3(4,﹣ ![]() ).
).
【解析】(1)根据折叠图形的轴对称性,△CED、△CBD全等,首先在Rt△CEO中求出OE的长,进而可得到AE的长;在Rt△AED中,AD=AB﹣BD、ED=BD,利用勾股定理可求出AD的长.进一步能确定D点坐标,利用待定系数法即可求出抛物线的解析式.(2)由于∠DEC=90°,首先能确定的是∠AED=∠OCE,若以P、Q、C为顶点的三角形与△ADE相似,那么∠QPC=90°或∠PQC=90°,然后在这两种情况下,分别利用相似三角形的对应边成比例求出对应的t的值.(3)由于以M,N,C,E为顶点的四边形,边和对角线都没明确指出,所以要分情况进行讨论:①EC做平行四边形的对角线,那么EC、MN必互相平分,由于EC的中点正好在抛物线对称轴上,所以M点一定是抛物线的顶点;②EC做平行四边形的边,那么EC、MN平行且相等,首先设出点N的坐标,然后结合E、C的横、纵坐标差表示出M点坐标,再将点M代入抛物线的解析式中,即可确定M、N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各所示:项目的工作量如图:

(1)从统计图中可知:擦玻璃的面积占总面积的百分比为 , 每人每分钟擦课桌椅m2;
(2)扫地拖地的面积是m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.

(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.

(1)求证:PC是⊙O的切线;
(2)求证:BC= AB;
AB;
(3)点M是 的中点,CM交AB于点N,若AB=4,求MNMC的值.
的中点,CM交AB于点N,若AB=4,求MNMC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( ) ①面积之比为1:2的两个相似三角形的周长之比是1:4;②三视图相同的几何体是正方体;③﹣27没有立方根;④对角线互相垂直的四边形是菱形;⑤某中学人数相等的甲、乙两班学生参加了同一次数学测验,班平均分和方差分别为
 =82分,
=82分,  =82分,S2甲=245,S2乙=190,那么成绩较为整齐的是乙班.
=82分,S2甲=245,S2乙=190,那么成绩较为整齐的是乙班.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论: ①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )

A.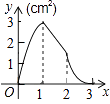
B.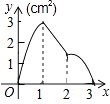
C.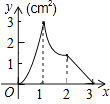
D.
相关试题

