【题目】某八年级计划用360元购买笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,结果买得的笔记本比打折前多10本.
(1)请利用分式方程求出每本笔记本的原来标价;
(2)恰逢文具店周年志庆,每本笔记本可以按原价打8折,这样该校最多可购入本笔记本?
参考答案:
【答案】(1)4元;(2)该校最多可购入112本笔记本.
【解析】
(1)设打折前售价为x元,则打折后售价为0.9x元,表示出打折前购买的数量及打折后购买的数量,再由打折后购买的数量比打折前多10本,可得出方程,解出即可.
(2)每本笔记本可以按原价打8折,即每本(4×0.8)元,360元除以打8折后每本的价格即可.
解:(1)设每本笔记本原来标价为x元,则打折后售价为0.9x元,
由题意得:![]() +10=
+10=![]() ,
,
解得:x=4,
经检验,x=4是原方程的根.
答:每本笔记本原来标价为4元;
(2)购入笔记本的数量为:360÷(4×0.8)=112.5
故该校最多可购入112本笔记本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将半径为4,圆心角为90°的扇形BAC绕A点逆时针旋转60°,点B、C的对应点分别为点D、E且点D刚好在
 上,则阴影部分的面积为_____.
上,则阴影部分的面积为_____.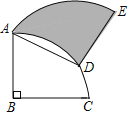
-
科目: 来源: 题型:
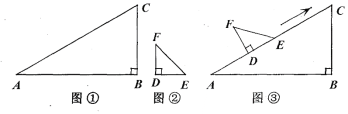
查看答案和解析>>【题目】某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.在图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°.图③是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
(1)在△DEF沿AC方向移动的过程中,该同学发现:F、C两点间的距离逐渐 ;连接FC,∠FCE的度数逐渐 .(填“不变”、“变大”或“变小”)
(2)△DEF在移动的过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;
(3)能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,
 平分
平分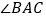 ,
,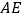 ⊥
⊥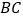 ,∠B=450,∠C=730.
,∠B=450,∠C=730. (1) 求
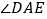 的度数;
的度数;(2) 如图②,若把“
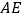 ⊥
⊥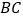 ”变成“点F在DA的延长线上,
”变成“点F在DA的延长线上,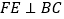 ”,其它条件不变,求
”,其它条件不变,求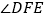 的度数;
的度数;(3) 如图③,若把“
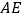 ⊥
⊥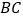 ”变成“
”变成“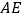 平分
平分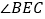 ”,其它条件不变,
”,其它条件不变, 的大小是否变化,并请说明理由.
的大小是否变化,并请说明理由.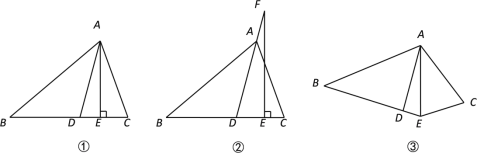
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AC=6,线段BC=15,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
解:∵M是AC的中点,AC=6,
∴MC=
 ______(填线段名称)=______,
______(填线段名称)=______,又因为CN:NB=1:2,BC=15,
∴CN=
 ______(填线段名称)=______.
______(填线段名称)=______.∴MN=______(填线段名称)+______(填线段名称)=8
∴MN的长为8.
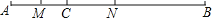
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连结BD,CD,其中CD交直线AP与点E.
(1)如图1,若∠PAB=30°,则∠ACE= ;
(2)如图2,若60°<∠PAB<120°,请补全图形,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并说明理由.

相关试题

