搜索
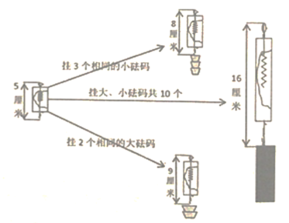
【题目】我们知道在一定条件下,弹簧的伸长量跟所挂物体质量成正比,根据图中给出的信息,解答下列问题:
(1)挂一个小砝码弹簧伸长 
,挂一个大砝码弹簧伸长 .
(2)如果要使弹簧长度为
,应挂大砝码、小砝码各多少个？
参考答案：
【答案】（1）1；2；（2）挂大砝码1个，则挂小砝码9个
【解析】
（1）根据图中信息，即可分别求出结论；
（2）设挂大砝码x个，则挂小砝码（10－x）个，根据题意列出方程，解方程即可得出结论．
解：（1）根据图中信息可知：挂一个小砝码弹簧伸长（8－5）÷3=1cm
挂一个大砝码弹簧伸长（9－5）÷2=2cm
故答案为：1；2．
（2）设挂大砝码x个，则挂小砝码（10－x）个
根据题意可得：5＋2x＋（10－x）=16
解得：x=1
则挂小砝码10－1=9个
答：挂大砝码1个，则挂小砝码9个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，2分别是某款篮球架的实物图与示意图，已知底座BC=0.60米，底座BC与支架AC所成的角∠ACB=75°，支架AF的长为2.50米，篮板顶端F点到篮框D的距离FD=1.35米，篮板底部支架HE与支架AF所成的角∠FHE=60°，求篮框D到地面的距离（精确到0.01米）（参考数据：cos75°≈0.2588，sin75°≈0.9659，tan75°≈3.732，
≈1.732，
≈1.414）
-
科目： 来源： 题型：
查看答案和解析>>【题目】李明准备进行如下操作实验，把一根长40 cm的铁丝剪成两段，并把每段首尾相连各围成一个正方形．
(1)要使这两个正方形的面积之和等于58 cm2，李明应该怎么剪这根铁丝？
(2)李明认为这两个正方形的面积之和不可能等于48 cm2，你认为他的说法正确吗？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=kx+6分别与x轴、y轴交于点E，F，已知点E的坐标为（﹣8，0），点A的坐标为（﹣6，0）．
（1）求k的值；
（2）若点P（x，y）是该直线上的一个动点，且在第二象限内运动，试写出△OPA的面积S关于x的函数解析式，并写出自变量x的取值范围．
（3）探究：当点P运动到什么位置时，△OPA的面积为
，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有8筐白菜，以每筐25千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后的纪录如下：
回答下列问题：
（1）这8筐白菜中最接近标准重量的这筐白菜重__________千克；
（2）与标准重量比较，8筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价2.6元，则出售这8筐白菜可卖多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，E、F是对角线BD上两点，且∠EAF=45°，将△ADF绕点A顺时针旋转90°后，得到△ABQ，连接EQ，求证：
（1）EA是∠QED的平分线；
（2）EF2=BE2+DF2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】今年水果大丰收，A，B两个水果基地分别收获水果380件、320件，现需把这些水果全部运往甲、乙两销售点，从A基地运往甲、乙两销售点的费用分别为每件40元和20元，从B基地运往甲、乙两销售点的费用分别为每件15元和30元，现甲销售点需要水果400件，乙销售点需要水果300件．
（1）设从A基地运往甲销售点水果x件，总运费为W元，请用含x的代数式表示W，并写出x的取值范围；
（2）若总运费不超过18300元，且A地运往甲销售点的水果不低于200件，试确定运费最低的运输方案，并求出最低运费．
相关试题
