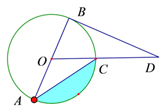
【题目】如图,BD是⊙O的切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4.
(1) 求∠BAC的大小;
(2) 求图中阴影部分的面积.
参考答案:
【答案】(1)30°;(2) ![]()
【解析】试题分析:(1)先由切线的性质得出∠DBA=90°,根据直角三角形的两锐角互余求出∠BOC=60°,然后根据同弧所对的圆周角是圆心角的一半即可得出答案;
(2)由条件可求得∠COA的度数,过O作OE⊥CA于点E,则可求得OE的长和CA的长,再利用S阴影=S扇形COA-S△COA可求得答案.
试题解析:
解:(1)∵DB为⊙O的切线,
∴![]() ,
,
∵![]()
![]()
∴![]() ;
;
(2)如图,过O作OE⊥CA于点E,

∵![]()
∴![]()
∵![]()
![]()
∴OE=2,
∴![]() ,
,
![]() ,
,
∴![]() 阴影=
阴影=![]() 扇形COA﹣
扇形COA﹣![]() △COA=
△COA=![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将正方形
 置于平面直角坐标系中,其中
置于平面直角坐标系中,其中 边在
边在 轴上,其余各边均与坐标轴平行.直线
轴上,其余各边均与坐标轴平行.直线 沿
沿 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形
轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形 的边所截得的线段长为
的边所截得的线段长为 ,平移的时间为
,平移的时间为 (秒),
(秒), 与
与 的函数图象如图2所示,则图1中的点
的函数图象如图2所示,则图1中的点 的坐标为__________,图2中
的坐标为__________,图2中 的值为__________.
的值为__________.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
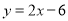 与反比例函数
与反比例函数 的图象交于点
的图象交于点 ,与
,与 轴交于点
轴交于点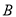 .
.(1)求
 的值及点
的值及点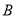 的坐标;
的坐标;(2)过点
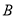 作
作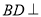
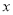 轴交反比例函数的图象于点
轴交反比例函数的图象于点 ,求点D的坐标和
,求点D的坐标和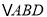 的面积;
的面积;(3)观察图象,写出当x>0时不等式
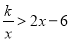 的解集.
的解集.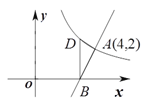
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…则第n个图形有__个小圆.

-
科目: 来源: 题型:
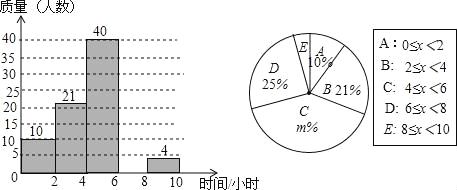
查看答案和解析>>【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 分别与x轴,y轴相交于A,B两点,0为坐标原点,A点的坐标为(4,0)
分别与x轴,y轴相交于A,B两点,0为坐标原点,A点的坐标为(4,0)(1)求k的值;
(2)过线段AB上一点P(不与端点重合)作x轴,y轴的垂线,乖足分别为M,N.当长方形PMON的周长是10时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)某自行车厂一周计划生产700辆自行车,平均每天生产自行车100辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入。下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆):
星期
一
二
三
四
五
六
日
增减
+8
-2
-3
+16
-9
+10
-11
(1)根据记录可知前三天共生产自行车 辆;
(2)产量最多的一天比产量最少的一天生产 辆;
(3)若该厂实行按生产的自行车数量的多少计工资,即计件工资制。如果每生产一辆自行车就可以得人民币60 元,超额完多成任务,每超一辆可多得 15 元;若不足计划数的,每少生产一辆扣 15 元,那么该厂工人这一周的工资总额是多少?
相关试题

