【题目】阅读：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为,当A、B两点中有一点在原点时，不妨设点A在原点，如图1，∣AB∣＝∣OB∣＝∣b∣＝∣a－b∣；

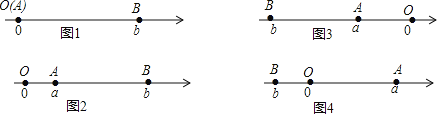
当A、B两点都不在原点时，如图2，点A、B都在原点的右边∣AB∣=∣OB∣－∣OA∣=∣b∣－∣a∣=b－a=∣a－b∣；如图3，点A、B都在原点的左边，∣AB∣＝∣OB∣－∣OA∣＝∣b∣－∣a∣=－b－（－a）=∣a－b∣；如图4，点A、B在原点的两边，∣AB∣＝∣OB∣+∣OA∣＝∣a∣+∣b∣= a +（－b）=∣a－b∣；

回答下列问题：

（1）数轴上表示3和5的两点之间的距离是_________,数轴上表示－3和－5的两点之间的距离是_________,数轴上表示1和－2的两点之间的距离是 ；

（2）数轴上表示x和－1的两点A和B之间的距离是 ,如果∣AB∣＝3，那么x为 ；

（3）当代数式∣x+3∣+∣x－2∣取最小值时，相应的x的取值范围是 ；当为 时，该代数式为7.

参考答案：

【答案】（1）2，2，3；（2），2或-4；（3），-4或3.

【解析】

（1）（2）根据数轴上A、B两点之间的距离，代入数值即可求出；

（3）代数式的最小值，意思是数轴上数x到－3的距离与到2 的距离之和最小，据此即可求出x的范围；若，在中间的时候代数式的值是5，只要在－3的左侧和2的右侧各找到一个到最近点距离为1的点就是所求.

解：（1）数轴上表示3和5的两点之间的距离是；

数轴上表示－3和－5的两点之间的距离是；

数轴上表示1和－2的两点之间的距离是；

（2）数轴上表示x和－1的两点A和B之间的距离是；

如果，则，所以或，解得：x=2或-4；

（3）代数式的最小值，意思是数轴上数x到－3的距离与到2 的距离之和最小，那么x应在－3与2之间的线段上，所以，这个最小值是；

若，在时，=5，所以只要在数轴上－3的左侧和2的右侧各找到一个到－3的距离和到2的距离为1的点就是所求，在数轴上－3的左侧的数是－4，2的右侧的数是3，所以当x=－4或3时，.

关闭