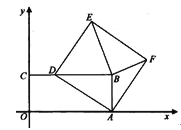
【题目】如图,在平面直角坐标系xoy中,矩形OABC的顶点B坐标为(12,5),点D在 CB边上从点C运动到点B,以AD为边作正方形ADEF,连BE、BF,在点D运动过程中,请探究以下问题:
(1)△ABF的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
(2)若△BEF为等腰三角形,求此时正方形ADEF的边长;
(3)设E(x,y),直接写出y关于x的函数关系式及自变量x的取值范围.
参考答案:
【答案】(1)不变,![]() ,理由见解析;(2)5
,理由见解析;(2)5![]() 或
或![]() 或
或![]() ;(3)y=-x+22(5
;(3)y=-x+22(5![]() x
x![]() 17)
17)
【解析】
(1)由“SAS”可证△ABD≌△FHA,可得HF=AB=5,即可求△ABF的面积;
(2)分三种情况讨论,由等腰三角形的性质和勾股定理可求正方形ADEF的边长;
(3)由全等三角形的性质,DH=AB=5,EH=DB,可得y=EH+5=DB+5,x=12-DB+DH=17-DB,即可求y关于x的函数关系式.
解:(1)作FH⊥AB交AB延长线于H,
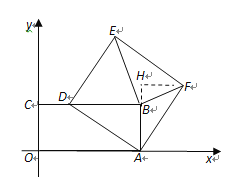
∵正方形ADEF中,AD=AF,∠DAF=90°,
∴∠DAH+∠FAH=90°.
∵∠H=90°,
∴∠FAH+∠AFH=90°,
∴∠DAH=∠AFH,
∵矩形OABC中,AB=5,∠ABD=90°,
∴∠ABD=∠H∴△ABD≌△FHA,
∴FH=AB=5,
∴![]() ;
;
(2)①当EB=EF时,作EG⊥CB
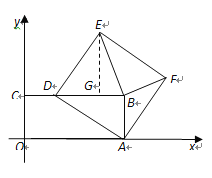
∵正方形ADEF中,ED=EF,
∴ED=EB ,
∴DB=2DG,
同(1)理得△ABD≌△GDE,
∴DG=AB=5 , ∴ DB=10,
∴![]() ;
;
②当EB=BF时,∠BEF=∠BFE,
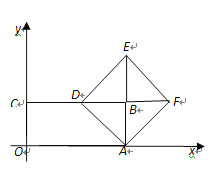
∵正方形ADEF中,ED=AF,∠DEF=∠AFE=90°,
∴∠BED=∠BFA,
∴△ABF≌△DBE,
∴BD=AB=5 ,
∵矩形OABC中,∠ABD=90°,
∴ ![]() ;
;
③当FB=FE时,作FQ⊥AB,
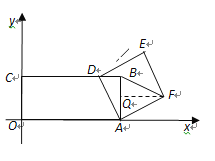
同理得BQ=AQ=![]() , BD=AQ=
, BD=AQ=![]() ,
,
∴![]() ;
;
(3)当5≤x≤12时,如图,
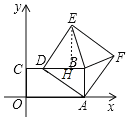
由(2)可知DH=AB=5,EH=DB,且E(x,y),
∴y=EH+5=DB+5,x=12-DB+DH=17-DB,
∴y=22-x,
当12<x≤17时,如图,
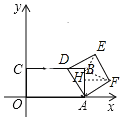
同理可得:x=12-DB+5=17-DB,y=DB+5,
∴y=22-x,
综上所述:当5≤x≤17时,y=22-xy=-x+22(5![]() x
x![]() 17).
17).
-
科目: 来源: 题型:
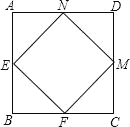
查看答案和解析>>【题目】E、F、M、N分别是正方形ABCD四条边上的点,AE=BF=CM=DN,四边形EFMN是什么图形?证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数 y =kx2 +(k +1)x +1(k 为实数),
(1)当 k=3 时,求此函数图象与 x 轴的交点坐标;
(2)判断此函数与 x 轴的交点个数,并说明理由;
(3)当此函数图象为抛物线,且顶点在 x 轴下方,顶点到 y 轴的距离为 2,求 k 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,位于第二象限的点
中,位于第二象限的点 在反比例函数
在反比例函数 的图像上,点
的图像上,点 与点
与点 关于原点
关于原点 对称,直线
对称,直线 经过点
经过点 ,且与反比例函数
,且与反比例函数 的图像交于点
的图像交于点 .
.
(1)当点
 的横坐标是-2,点
的横坐标是-2,点 坐标是
坐标是 时,分别求出
时,分别求出 的函数表达式;
的函数表达式;(2)若点
 的横坐标是点
的横坐标是点 的横坐标的4倍,且
的横坐标的4倍,且 的面积是16,求
的面积是16,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】)图①中是一座钢管混凝土系杆拱桥,桥的拱肋ACB可视为抛物线的一部分(如图②),桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋
的跨度AB为200米,与AB中点O相距20米处有一高度为48米的系杆.
【1】求正中间系杆OC的长度;
【2】若相邻系杆之间的间距均为5米(不考虑系杆的粗细),则是否存在一根系杆的长度恰好是OC长度的一半?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.

(1)在图1中,EF=___,BF=____;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的S1,S2,若m-n=2,请问S2-S1的值为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
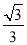 x﹣
x﹣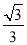 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
相关试题

