【题目】如图,△ABC中,∠A=40°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF= 度.

参考答案:
【答案】75
【解析】
试题分析:首先根据三角形的内角和定理求得∠ACB的度数,以及∠BCD的度数,根据角平分线的定义求得∠BCE的度数,则∠ECD可以求解,然后在△CDF中,利用内角和定理即可求得∠CDF的度数.
∵∠A=40°,∠B=70°, ∴∠ACB=180°﹣∠A﹣∠B=70°. ∵CE平分∠ACB,
∴∠ACE=![]() ∠ACB=35°. ∵CD⊥AB于D, ∴∠CDA=90°, ∠ACD=180°﹣∠A﹣∠CDA=50°.
∠ACB=35°. ∵CD⊥AB于D, ∴∠CDA=90°, ∠ACD=180°﹣∠A﹣∠CDA=50°.
∴∠ECD=∠ACD﹣∠ACE=15°. ∵DF⊥CE, ∴∠CFD=90°, ∴∠CDF=180°﹣∠CFD﹣∠DCF=75°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学为了深入学习社会主义核心价值观,特对本校部分学生(随机抽样)进行了一次相关知识的测试(成绩分为A、B、C、D、E、五个组,x表示测试成绩),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题.
A组:90≤x≤100 B组:80≤x<90 C组:70≤x<80 D组:60≤x<70 E组:x<60
(1)参加调查测试的学生共有人;请将两幅统计图补充完整 .
(2)本次调查测试成绩的中位数落在组内.
(3)本次调查测试成绩在80分以上(含80分)为优秀,该中学共有3000人,请估计全校测试成绩为优秀的学生有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为( )
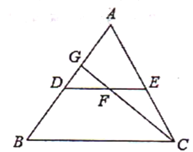
A.4cm2 B.6cm2 C.8cm2 D.9cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“<”“>”或“=”号填空:
(1)﹣
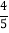 _____﹣
_____﹣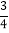 ;
; (2)﹣(﹣0.01)_____ (﹣
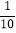 )2;
)2; (3)3.9950(精确到0.01)_____3.999.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由相同的花盆按一定的规律组成的正多边形图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…,则第n个图形中花盆的个数为_____.
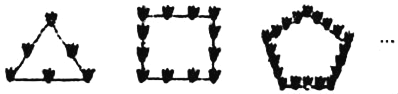
-
科目: 来源: 题型:
查看答案和解析>>【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,
 ≈1.414,
≈1.414, 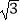 ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米). 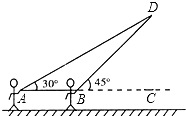
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?
相关试题

