【题目】如图,平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证:
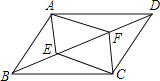
(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
参考答案:
【答案】见解析
【解析】
试题分析:(1)根据平行四边形平行四边形的性质得到AB∥CD AB=CD,从而得到∠ABE=∠CDF,然后利用SAS证得两三角形全等即可;
(2)利用(1)中的全等三角形的对应角相等推知∠AEB=∠DFC,则等角的补角相等,即∠AEF=∠CFE,所以AE∥FC.根据“有一组对边平行且相等”证得结论.
证明(1)∵四边形ABCD是平行四边形,
∴AB∥CD AB=CD,
∴∠ABE=∠CDF,
∵BE=DF,
∴△ABE≌△CDF (SAS);
(2)证明:∵由(1)知,△ABE≌△CDF,
∴BE=DF,∠AEB=∠DFC,
∴∠AEF=∠CFE,
∴AE∥FC,
∴四边形AECF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车销售公司经销某品牌A、B两款汽车,已知A款汽车每辆进价为
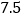 万元,B款汽车每辆进价为6万元.
万元,B款汽车每辆进价为6万元.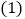 公司预计用不多于135万元且不少于129万元的资金购进这两款汽车共20辆,有几种进货方案,它们分别是什么?
公司预计用不多于135万元且不少于129万元的资金购进这两款汽车共20辆,有几种进货方案,它们分别是什么?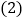 如果A款汽车每辆售价为9万元,B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使
如果A款汽车每辆售价为9万元,B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使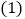 中所有的方案获利相同,a值应是多少,此种方案是什么?(提示:可设购进B款汽车x辆)
中所有的方案获利相同,a值应是多少,此种方案是什么?(提示:可设购进B款汽车x辆) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)(+16)+(-25)-(-24)+(-32)
(2)(-26.54)-︱-6.4︱+18.54+6.4
(3)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
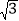 x+4
x+4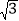 分别与x轴,y轴相交于点A,B,点C在直线AB上,D是坐标平面内一点,若以点O,A,C,D为顶点的四边形是菱形,则点D的坐标是_____.
分别与x轴,y轴相交于点A,B,点C在直线AB上,D是坐标平面内一点,若以点O,A,C,D为顶点的四边形是菱形,则点D的坐标是_____.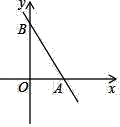
-
科目: 来源: 题型:
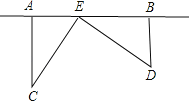
查看答案和解析>>【题目】为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.Okm,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】东方红中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向西走100米到聪聪家,再向东走150米到青青家,再向西走200米到刚刚家,请问:
(1)如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出聪聪家与青青家的大概位置(数轴上一格表示50米).
(2)聪聪家与刚刚家相距多远?
(3)聪聪家向西20米所表示的数是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若表示﹣1的点与表示3的点重合,回答以下问题:
①表示5的点与表示数_________的点重合;
②若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
(2)若点D表示的数为x,则当x为_______时,|x+1|与|x﹣2|的值相等.

相关试题

