Question

【题目】按要求完成下列证明
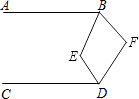
如图，AB∥CD，CB∥DE，求证：∠B+∠D=180°．
证明：∵AB∥CD，
∴∠B=（）．
∵CB∥DE，
∴∠C+=180°（）．
∴∠B+∠D=180°．

Answer 1

【答案】∠C；两直线平行，内错角相等；∠D；两直线平行，同旁内角互补
【解析】证明：∵AB∥CD，
∴∠B=∠C （两直线平行，内错角相等），
∵CB∥DE，
∴∠C+∠D=180°（两直线平行，同旁内角互补），
∴∠B+∠D=180°．
所以答案是：∠C，两直线平行，内错角相等；∠D；两直线平行，同旁内角互补．
【考点精析】利用平行线的性质对题目进行判断即可得到答案，需要熟知两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．