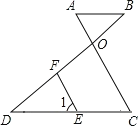
【题目】一副三角板如图1摆放,∠C=∠DFE=90,∠B=30,∠E=45,点F在BC上,点A在DF上,且AF平分∠CAB,现将三角板DFE绕点F顺时针旋转(当点D落在射线FB上时停止旋转).

(1)当∠AFD=_ __时,DF∥AC;当∠AFD=__ _时，DF⊥AB；

(2)在旋转过程中，DF与AB的交点记为P，如图2，若AFP有两个内角相等，求∠APD的度数；

(3)当边DE与边AB、BC分别交于点M、N时，如图3，若∠AFM=2∠BMN，比较∠FMN与∠FNM的大小，并说明理由。

参考答案：

【答案】(1)30；60(2) 60或105或150(3)∠FMN=∠FNM

【解析】分析：（1）当∠AFD=30°时，AC∥DF，依据角平分线的定义可先求得∠CAF=∠FAB=30°，由内错角相等，两直线平行，可证明AC∥DF，；当∠AFD=60°时，DF⊥AB，由三角形的内角和定理证明即可；

（2）分为∠FAP=∠AFP，∠AFP=∠APF，∠APF=∠FAP三种情况求解即可；

（3）先依据三角形外角的性质证明∠FNM=30°+∠BMN，接下来再依据三角形外角的性质以及∠AFM和∠BMN的关系可证明∠FMN=30°+∠BMN，从而可得到∠FNM与∠FMN的关系．

详解：（1）如图1所示：

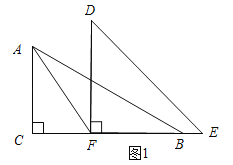
当∠AFD=30时，AC∥DF．

理由：∵∠CAB=60°，AF平分∠CAB，∴∠CAF=30°．

∵∠AFD=30°，∴∠CAF=∠AFD，∴AC∥DF．

如图2所示：当∠AFD=60°时，DF⊥AB．

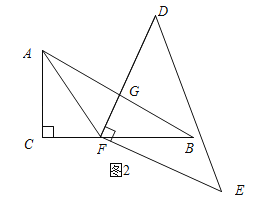
∵∠CAB=60°，AF平分∠CAB，∴∠AFG=30°．

∵∠AFD=60°，∴∠FGB=90°，∴DF⊥AB．

故答案为：30；60．

（2）∵∠CAB=60°，AF平分∠CAB，∴∠FAP=30°．

当如图3所示：

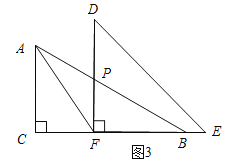
当∠FAP=∠AFP=30°时，∠APD=∠FAP+∠AFP=30°+30°=60°；

如图4所示：

当∠AFP=∠APF时．

∵∠FAP=30°，∠AFP=∠APF，∴∠AFP=∠APF=×（180°﹣30°）=×150°=75°，∴∠APD=∠FAP+∠AFP=30°+75°=105°；

如图5所示：

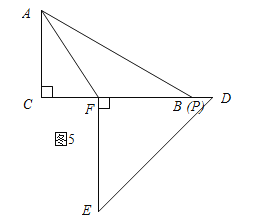
如图5所示：当∠APF=∠FAP=30°时．

∠APD=180°﹣30°=150°．

综上所述：∠APD的度数为60°或105°或150°．

（3）∠FMN=∠FNM．

理由：如图6所示：

∵∠FNM是△BMN的一个外角，∴∠FNM=∠B+∠BMN．

∵∠B=30°，∴∠FNM=∠B+∠BMN=30°+∠BMN．

∵∠BMF是△AFM的一个外角，∴∠MBF=∠MAF+∠AFM，即∠BMN+∠FMN=∠MAF+∠AFM．

又∵∠MAF=30°，∠AFM=2∠BMN，∴∠BMN+∠FMN=30°+2∠BMN，∴∠FMN=30°+∠BMN，∴∠FNM=∠FMN．

关闭