【题目】△ABC中,AB=12,AC= ![]() ,∠B=30°,则△ABC的面积是 .
,∠B=30°,则△ABC的面积是 .
参考答案:
【答案】21 ![]() 或15
或15 ![]()
【解析】解:①如图1,作AD⊥BC,垂足为点D, 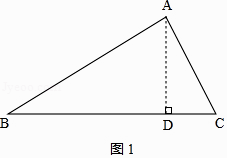
在Rt△ABD中,∵AB=12、∠B=30°,
∴AD= ![]() AB=6,BD=ABcosB=12×
AB=6,BD=ABcosB=12× ![]() =6
=6 ![]() ,
,
在Rt△ACD中,CD= ![]() =
= ![]() =
= ![]() ,
,
∴BC=BD+CD=6 ![]() +
+ ![]() =7
=7 ![]() ,
,
则S△ABC= ![]() ×BC×AD=
×BC×AD= ![]() ×7
×7 ![]() ×6=21
×6=21 ![]() ;②如图2,作AD⊥BC,交BC延长线于点D,
;②如图2,作AD⊥BC,交BC延长线于点D,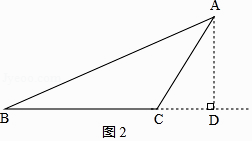
由①知,AD=6、BD=6 ![]() 、CD=
、CD= ![]() ,
,
则BC=BD﹣CD=5 ![]() ,
,
∴S△ABC= ![]() ×BC×AD=
×BC×AD= ![]() ×5
×5 ![]() ×6=15
×6=15 ![]() ,
,
故答案为:21 ![]() 或15
或15 ![]() .
.
过A作AD⊥BC于D(或延长线于D),根据含30度角的直角三角形的性质得到AD的长,再根据勾股定理得到BD,CD的长,再分两种情况:如图1,当AD在△ABC内部时、如图2,当AD在△ABC外部时,进行讨论即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD周长是( )
A.22
B.20
C.22或20
D.18 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( ) ①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2
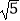 ﹣2.
﹣2.
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为4的正方形ABCD,点P是对角线BD上一动点,点E在边CD上,EC=1,则PC+PE的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣1,3),B(﹣3,1),C(﹣1,1).请解答下列问题:

(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出B1的坐标.
(2)画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1 , 并求出点A1走过的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=﹣
 x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD. 
(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD , 求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校在艺术节选拔节目过程中,从备选的“街舞”、“爵士”、“民族”、“拉丁”四种类型舞蹈中,选择一种学生最喜爱的舞蹈,为此,随机调查了本校的部分学生,并将调查结果绘制成如下统计图表(每位学生只选择一种类型),根据统计图表的信息,解答下列问题:
类型
民族
拉丁
爵士
街舞
据点百分比
a
30%
b
15%

(1)本次抽样调查的学生人数及a、b的值.
(2)将条形统计图补充完整.
(3)若该校共有1500名学生,试估计全校喜欢“拉丁舞蹈”的学生人数.
相关试题

