Question

【题目】如图，已知抛物线y=﹣x2+mx+3与x轴交于点A、B两点，与y轴交于C点，点B的坐标为（3，0），抛物线与直线y=﹣ x+3交于C、D两点．连接BD、AD．
（1）求m的值．
（2）抛物线上有一点P，满足S△ABP=4S△ABD ， 求点P的坐标．

Answer 1

【答案】
（1）解：∵抛物线y=﹣x2+mx+3过（3，0），

∴0=﹣9+3m+3，

∴m=2

（2）解：由 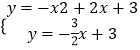，得 ， ，

∴D（ ，﹣ ），

∵S△ABP=4S△ABD，

∴ AB×|yP|=4× AB× ，

∴|yP|=9，yP=±9，

当y=9时，﹣x2+2x+3=9，无实数解，

当y=﹣9时，﹣x2+2x+3=﹣9，x1=1+ ，x2=1﹣ ，

∴P（1+ ，﹣9）或P（1﹣ ，﹣9）．

【解析】（1）利用待定系数法即可解决问题；（2）利用方程组首先求出点D坐标．由面积关系，推出点P的纵坐标，再利用待定系数法求出点P的坐标即可；
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识，掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．