【题目】某射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了8次测试,测试成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 10 | 8 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | 8 | 10 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙两名运动员8次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,并说明理由.
参考答案:
【答案】(1)9,9;(2) 甲的方差为:0.75,乙的方差为:1.25;(3) 甲比较稳定,故选甲参加全国比赛更合适
【解析】
(1)根据平均数的计算公式计算即可;
(2)利用方差公式计算;
(3)根据方差反映了一组数据的波动大小,方差越大,波动性越大解答即可.
解:(1)甲的平均成绩为:![]() ×(10+8+9+8+10+9+10+8)=9,
×(10+8+9+8+10+9+10+8)=9,
乙的平均成绩为:![]() ×(10+7+10+10+9+8+8+10)=9
×(10+7+10+10+9+8+8+10)=9
(2)甲的方差为: [(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2+(10-9)2+(8-9)2]=0.75,
乙的方差为:![]() [(10-9)2+(7-9)2+(10-9)2+(10-9)2+(9-9)2+(8-9)2+(8-9)2+(10-9)2]=1.25,
[(10-9)2+(7-9)2+(10-9)2+(10-9)2+(9-9)2+(8-9)2+(8-9)2+(10-9)2]=1.25,
(3)甲、乙平均分相等,说明两人的水平相当
又∵0.75<1.25, ∴甲的方差小,
∴甲比较稳定,故选甲参加全国比赛更合适.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a是一个长为2m、宽为2n的长方形,沿图中实现用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.
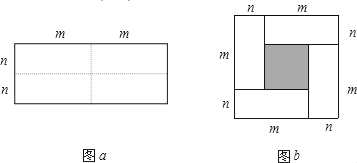
(1)图b中,大正方形的边长是 .阴影部分小正方形的边长是 ;
(2)观察图b,写出(m+n)2,(m﹣n)2,mn之间的一个等量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,将一个长方形沿着对角线剪开即可得到两个全等的三角形,再把△ABC沿着AC方向平移,得到图②中的△GBH,BG交AC于点E,GH交CD于点F.在图②中,除△ACD与△HGB全等外,你还可以指出哪几对全等的三角形(不能添加辅助线和字母)?请选择其中一对加以证明.
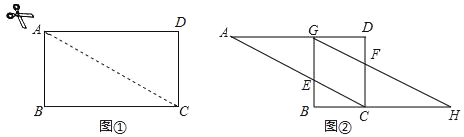
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在北京市治理违建的过程中,某小区拆除了自建房,改建绿地. 如图,自建房占地是边长为8m的正方形ABCD,改建的绿地是矩形AEFG,其中点E在AB上,点G在AD的延长线上,且DG = 2BE. 如果设BE的长为x(单位:m),绿地AEFG的面积为y(单位:m2),那么y与x的函数的表达式为__________________;当BE =______m时,绿地AEFG的面积最大.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是“过圆外一点作圆的切线”的尺规作图过程.



请回答以下问题:
(1)连接OA,OB,可证∠OAP =∠OBP = 90°,理由是______________________;
(2)直线PA,PB是⊙O的切线,依据是__________________________________.
相关试题

