【题目】设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,
(1)试推导x1+x2=-![]() ,x1·x2=
,x1·x2=![]() ;
;
(2)求代数式a(x13+x23)+b(x12+x22)+c(x1+x2)的值.
参考答案:
【答案】(1)x1+x2=-![]() ,x1·x2=
,x1·x2=![]() (2)0
(2)0
【解析】试题分析:(1)利用求根公式表示出x1,x2,代入所求式子可直接推导得出结论;
(2)把式子拆开重新整理成一元二次方程的形式,然后把x1,x2代入原方程,整体代入即可求出代数式的值.
解:(1)∵x1、x2是ax2+bx+c=0(a≠0)的两根,
∴x1=![]() ,x2=
,x2=![]()
∴x1+x2=![]() =-
=-![]() ,
,
x1·x2=![]() ·
·![]() =
=![]()
(2)∵x1,x2是ax2+bx+c=0的两根,∴ax12+bx1+c=0,ax22+bx2+c=0
原式=ax13+bx12+c1x1+ax23+bx22+cx2
=x1(ax12+bx1+c)+x2(ax22+bx2+c)
=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】去年11月份我市某一天的最高气温是15℃,最低气温是﹣1℃,那么这一天的最高气温比最低气温高( )
A. 16℃ B. ﹣15℃ C. 14℃ D. 13℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学老师在课堂上提出一个问题:“通过探究知道:
 ≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用
≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用 ﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:(1)
 的小数部分是a,
的小数部分是a,  的整数部分是b,求a+b﹣
的整数部分是b,求a+b﹣ 的值.
的值.(2)已知8+
 =x+y,其中x是一个整数,0<y<1,求3x+(y﹣
=x+y,其中x是一个整数,0<y<1,求3x+(y﹣ )2018的值.
)2018的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若三角形有两个内角的和是90°,那么这个三角形是( )
A.钝角三角形B.直角三角形C.角三角形D.不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为10的等边
 中,点
中,点 从点
从点 出发沿射线
出发沿射线 移动,同时点
移动,同时点 从点
从点 出发沿线段
出发沿线段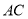 的延长线移动,点
的延长线移动,点 、
、 移动的速度相同,
移动的速度相同,  与直线
与直线 相交于点
相交于点 .
.(1)如图①,当点
 为
为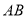 的中点时,
的中点时,(I)求证:
 ;(II)求
;(II)求 的长;
的长;


(2)如图②,过点
 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,当点
,当点 、
、 在移动的过程中,试确定
在移动的过程中,试确定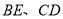 的数量关系,并说明理由.
的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电厂规定:该厂家属区的每户居民一个月用电量不超过A千瓦时,那么这户居民这个月只交10元电费,如果超过A千瓦时,那么这个月除了交10元用电费外超过部分还要按每千瓦时
 元收费.
元收费.(1)若某户2月份用电90千瓦时,超过规定A千瓦时,则超过部分电费为多少元?(用A表示)
(2)下表是这户居民3月、4月的用电情况和交费情况
月份
用电量(千瓦时)
交电费总金额(元)
3
80
25
4
45
10
根据上表数据,求电厂规定的A值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】从社会效益和经济效益出发,某地制定了三年规划,投入资金进行生态环境建设,并以此发展旅游产业。根据规划,第一年度投入资金800万元,第二年度比第一年度减少
 ,第三年度比第二年度减少
,第三年度比第二年度减少 。第一年度当地旅游业收入估计为400万元,要使三年内的投入资金与旅游业总收入持平,旅游业收入的年增长率应是多少?(以下数据供选用:
。第一年度当地旅游业收入估计为400万元,要使三年内的投入资金与旅游业总收入持平,旅游业收入的年增长率应是多少?(以下数据供选用:  =1.414,
=1.414,  =3.606 计算结果精确到百分位)
=3.606 计算结果精确到百分位)
相关试题

