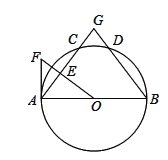
【题目】如图,AB是⊙O的直径,C、D为⊙O上两点,且![]() ,过点O作OE⊥AC于点E,⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
,过点O作OE⊥AC于点E,⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
(1)求证:∠F=∠B;
(2)若AB=10,BG=13,求AF的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据圆周角定理得到∠GAB=∠B,根据切线的性质得到∠GAB+∠GAF=90°,证明∠F=∠GAB,等量代换即可证明;
(2)连接OG,根据勾股定理求出OG,证明△FAO∽△BOG,根据相似三角形的性质列出比例式,计算即可.
(1)∵![]() ,
,
∴![]() ,
,
∴∠GAB=∠B,
∵AF是⊙O的切线,
∴AF⊥AO,
∴∠GAB+∠GAF=90°,
∵OE⊥AC,
∴∠F+∠GAF=90°,
∴∠F=∠GAB,
∴∠F=∠B;
(2)连接OG,
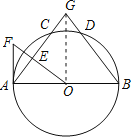
∵∠GAB=∠B,
∴AG=BG,
∵OA=OB=5,
∴OG⊥AB,
∴OG=![]() =
=![]() =8,
=8,
∵∠FAO=∠BOG=90°,∠F=∠B,
∴△FAO∽△BOG,
∴![]() ,
,
∴AF=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
 绕点
绕点 顺时针旋转得到
顺时针旋转得到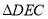 ,使点
,使点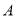 的对应点
的对应点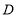 恰好落在边
恰好落在边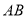 上,点
上,点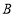 的对应点为
的对应点为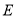 ,连接
,连接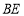 ,其中有:①
,其中有:①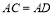 ;②
;②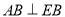 ;③
;③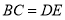 ;④
;④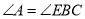 ,四个结论,则结论一定正确的有( )个
,四个结论,则结论一定正确的有( )个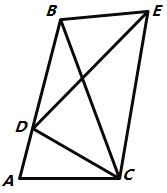
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲、乙两组,进行力四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如图统计图.
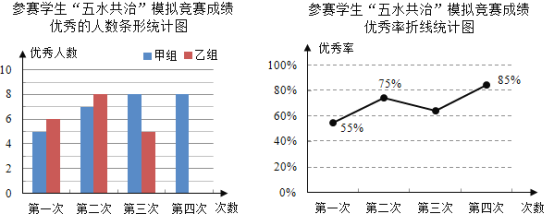
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整;
(2)已求得甲组成绩优秀人数的平均数
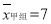 ,方差
,方差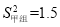 ,请通过计算说明,哪一组成绩优秀的人数比较稳定?
,请通过计算说明,哪一组成绩优秀的人数比较稳定? -
科目: 来源: 题型:
查看答案和解析>>【题目】从宁海县到某市,可乘坐普通列车或高铁,已知高铁的行驶路程与普通列车的行驶路程之和是920千米,而普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车的平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角梯形ABCD中,AD∥BC,∠B=∠A=90°,AD=a,BC=b,AB=c,
操作示例
我们可以取直角梯形ABCD的一腰CD的中点P,过点P作PE∥AB,裁掉△PEC,并将△PEC拼接到△PFD的位置,构成新的图形(如图2).
思考发现
小明在操作后发现,该剪拼方法就是先将△PEC绕点P逆时针旋转180°到△PFD的位置,易知PE与PF在同一条直线上.又因为在梯形ABCD中,AD∥BC,∠C+∠ADP=180°,则∠FDP+∠ADP=180°,所以AD和DF在同一条直线上,那么构成的新图形是一个四边形,进而根据平行四边形的判定方法,可以判断出四边形ABEF是一个平行四边形,而且还是一个特殊的平行四边形——矩形.
1.图2中,矩形ABEF的面积是 ;(用含a,b,c的式子表示)
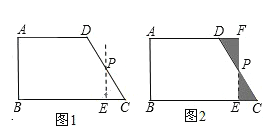
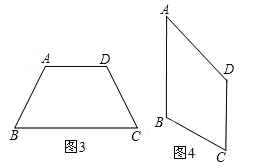
2.类比图2的剪拼方法,请你就图3(其中AD∥BC)和图4(其中AB∥DC)的两种情形分别画出剪拼成一个平行四边形的示意图.
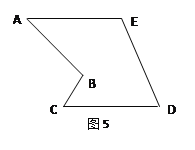
3.小明通过探究后发现:在一个四边形中,只要有一组对边平行,就可以剪拼成平行四边形.
如图5的多边形中,AE=CD,AE∥CD,能否象上面剪切方法一样沿一条直线进行剪切,拼成一个平行四边形?若能,请你在图中画出剪拼的示意图并作必要的文字说明;若不能,简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图I,在
 中,
中, .点
.点 在
在 外,连接
外,连接 ,作
,作 ,交
,交 于点
于点 ,
, ,
, ,连接
,连接 .则
.则 间的等量关系是______;(不用证明)
间的等量关系是______;(不用证明)(2)如图Ⅱ,
 ,
, ,
, ,延长
,延长 交
交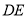 于点
于点 ,写出
,写出 间的等量关系,并证明你的结论.
间的等量关系,并证明你的结论.
相关试题

