【题目】(1)如图I,在![]() 中,
中,![]() .点
.点![]() 在
在![]() 外,连接
外,连接![]() ,作
,作![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() .则
.则![]() 间的等量关系是______;(不用证明)
间的等量关系是______;(不用证明)
(2)如图Ⅱ,![]() ,
,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,写出
,写出![]() 间的等量关系,并证明你的结论.
间的等量关系,并证明你的结论.

参考答案:
【答案】(1)DF=BC+CF;(2)BC=CF+DF;证明见详解.
【解析】
(1)根据题意可证△ABC≌ADE,△ACF≌△AEF,可得DE=BC,EF=FC,用等量代换可得三者之间的关系,
(2)连接AF,相应的证明△ABC≌ADE,△ACF≌△AEF,可得DE=BC,EF=FC,再利用等量代换可以得出DF,BC,CF间的等量关系.
解:(1)如图1,DF=BC+CF,
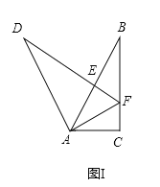
∵DE⊥AB,
∴∠AED=90°=∠AEF=∠ACB,
在Rt△ACF和△AEF中,
∵AC=AE,AF=AF,
∴Rt△ACF≌△AEF (HL),
∴CF=EF,
在Rt△ADE和△ABC中,
∵AD=AB,AC=AE,
∴Rt△ADE≌△ABC (HL),
∴DE=BC,
又∵DF=DE+EF,
∴DF=BC+CF.
故答案为:DF=BC+CF.
(2)BC=CF+DF
如图,连接AF,

∵AB=AD,AC=AE,∠ACB=∠AED=90°,
∵Rt△ADE≌△ABC (HL),
∴DE=BC,
又∵AE=AC,AF=AF,
∴Rt△ACF≌△AEF (HL),
∴CF=EF,
又∵DE=EF+DF,
∴BC=CF+DF,
答:DF,BC,CF间的等量关系为:BC=CF+DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈
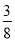 ,cos22°≈
,cos22°≈ ,tan22°≈
,tan22°≈ )
) -
科目: 来源: 题型:
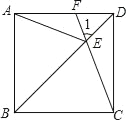
查看答案和解析>>【题目】如图,在正方形ABCD中,E是对角线BD上任意一点(BE>DE),CE的延长线交AD于点F,连接AE.
(1)求证:△ABE∽△FDE;
(2)当BE=3DE时,求tan∠1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.

(1)如图,当点E在BD上时.求证:FD=CD;
(2)当α为何值时,GC=GB?画出图形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 (x+m)(x﹣4)(m>0)交x轴于点A、B(A左B右),交y轴于点C,过点B的直线y=
(x+m)(x﹣4)(m>0)交x轴于点A、B(A左B右),交y轴于点C,过点B的直线y= x+b交y轴于点D.
x+b交y轴于点D.
(1)求点D的坐标;
(2)把直线BD沿x轴翻折,交抛物线第二象限图象上一点E,过点E作x轴垂线,垂足为点F,求AF的长;
(3)在(2)的条件下,点P为抛物线上一点,若四边形BDEP为平行四边形,求m的值及点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为开展全科大阅读活动,学校花费了3400元在书店购买了40套古典文学书籍和20套现代文学书籍,每套现代文学书籍比每套古典文学书籍多花20元.
(1)求每套古典文学习书籍和现代文学书籍分别是多少元?
(2)为满足学生的阅读需求,学校计划用不超过2500元再次购买古典文学和现代文学书籍共40套,经市场调查得知,每套古典文学书籍价格上浮了20%,每套现代文学书籍价格下调了10%,学校最多能购买多少套现代文学书籍?
相关试题

