【题目】在平面直角坐标系中,B点坐标为(x、y),且x、y满足|x+y﹣8|+(x﹣y)2=0.
(1)求B点坐标;
(2)如图,点A为y轴正半轴上一点,过点B作BC⊥AB,交x轴正半轴于点C,求证:AB=BC. 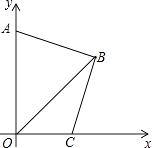
参考答案:
【答案】
(1)解:∵|x+y﹣8|+(x﹣y)2=0,
∴ ![]() ,
,
解得, ![]() ,
,
即点B的坐标为(4,4)
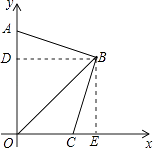
(2)解:作BD⊥OA于点D,作BE⊥OC于点E,如右图所示,
∵BC⊥AB,∠DBE=90°,∠ADB=∠CEB=90°,
∴∠ABC=90°,
∴∠ABD+∠DBC=∠DBC+∠CBE=90°,
∴∠ABD=∠CBE,
又∵点B(4,4),
∴BD=BE=4,
∴△ADB≌△CEB(ASA),
∴AB=BC.
【解析】(1)根据x、y满足|x+y﹣8|+(x﹣y)2=0,可以求得x、y的值,从而可以求得点B的坐标;(2)根据题意,可以作辅助线,只要证明△ADB≌△CEB即可证明AB与BC的关系,根据题目中的条件可以得到△ADB≌△CEB的条件,本题得以解决.
【考点精析】掌握解二元一次方程组是解答本题的根本,需要知道二元一次方程组:①代入消元法;②加减消元法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明想把一长为25cm,宽为20cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.

(1)若设小正方形的边长为x cm,用含x的代数式表示图中阴影部分的面积;
(2)当x=5时,求这个盒子的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第一次点A向左移动3个单位长度至点A1 , 第2次从点A1向右移动6个单位长度至点A2 , 第3次从点A2向左移动9个单位长度至点A3 , …,按照这种移动方式进行下去,点A4表示的数是 , 如果点An与原点的距离不小于20,那么n的最小值是 .
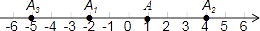
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(2x﹣1)(1﹣2x)结果正确的是( )
A.4x2﹣1
B.1﹣4x2
C.﹣4x2+4x﹣1
D.4x2﹣4x+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】正六边形一个外角是______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料并解决有关问题:
我们知道:|x|= .现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
①x<﹣1;②﹣1≤x<2;③x≥2.
从而化简代数式|x+1|+|x﹣2|可分以下3种情况:
①当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②当﹣1≤x<2时,原式=x+1﹣(x﹣2)=3;
③当x≥2时,原式=x+1+x﹣2=2x﹣1.综上讨论,原式= .
.
通过以上阅读,请你解决以下问题:
(1)化简代数式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)12﹣7+18﹣15
(2) ÷(﹣
÷(﹣  )×(﹣1
)×(﹣1 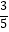 )
)
(3)( ﹣
﹣  +
+ 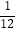 )×(﹣48)
)×(﹣48)
(4)﹣24+(﹣5)2÷(﹣1 )
)
相关试题

