【题目】阅读下面材料并解决有关问题:
我们知道:|x|=  .现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
①x<﹣1;②﹣1≤x<2;③x≥2.
从而化简代数式|x+1|+|x﹣2|可分以下3种情况:
①当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②当﹣1≤x<2时,原式=x+1﹣(x﹣2)=3;
③当x≥2时,原式=x+1+x﹣2=2x﹣1.综上讨论,原式=  .
.
通过以上阅读,请你解决以下问题:
(1)化简代数式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
参考答案:
【答案】
(1)解:当x<﹣2时,|x+2|+|x﹣4|=﹣x﹣2+4﹣x=﹣2x+2;
当﹣2≤x<4时,|x+2|+|x﹣4|=x+2+4﹣x=6;
当x≥4时,|x+2|+|x﹣4|=x+2+x﹣4=2x﹣2
(2)解:当x<﹣1时,原式=3x+5<2,
当﹣1≤x≤1时,原式=﹣5x﹣3,﹣8≤﹣5x﹣3≤2,
当x>1时,原式=﹣3x﹣5<﹣8,
则|x﹣1|﹣4|x+1|的最大值为2
【解析】(1)分为x<﹣2、﹣2≤x<4、x≥4三种情况化简即可;(2)分x<﹣1、﹣1≤x≤1、x>1分别化简,结合x的取值范围确定代数式值的范围,从而求出代数式的最大值.
【考点精析】本题主要考查了绝对值的相关知识点,需要掌握正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(2x﹣1)(1﹣2x)结果正确的是( )
A.4x2﹣1
B.1﹣4x2
C.﹣4x2+4x﹣1
D.4x2﹣4x+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,B点坐标为(x、y),且x、y满足|x+y﹣8|+(x﹣y)2=0.
(1)求B点坐标;
(2)如图,点A为y轴正半轴上一点,过点B作BC⊥AB,交x轴正半轴于点C,求证:AB=BC.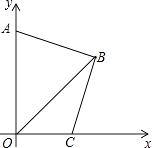
-
科目: 来源: 题型:
查看答案和解析>>【题目】正六边形一个外角是______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)12﹣7+18﹣15
(2) ÷(﹣
÷(﹣  )×(﹣1
)×(﹣1 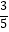 )
)
(3)( ﹣
﹣  +
+ 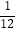 )×(﹣48)
)×(﹣48)
(4)﹣24+(﹣5)2÷(﹣1 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四边形不属于平行四边形的是( )
A.菱形B.矩形C.梯形D.正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
相关试题

