【题目】6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图. 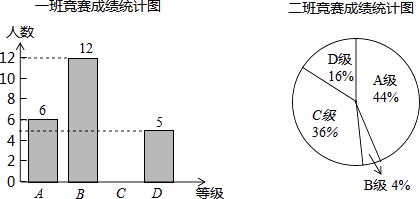
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | d | 80 | c |
(1)把一班竞赛成绩统计图补充完整;
(2)写出表中a、b、c的值:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | d | 80 | c |
(3)请从平均数和中位数方面比较一班和二班的成绩,对这次竞赛成绩的结果进行分析.
参考答案:
【答案】
(1)解:一班C等级的人数为25﹣6﹣12﹣5=2(人),
统计图为:
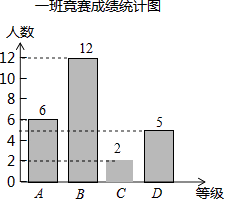
(2)解:一班的平均数a= ![]() (6×100+12×90+2×80+5×70)=87.6(分),
(6×100+12×90+2×80+5×70)=87.6(分),
b=90(分);
二班A等级的人数为44%×25=11(人),B等级的人数为4%×25=1(人),C等级的人数为36%×25=9(人),D等级的人数为16%×25=4(人),
d= ![]() (11×100+1×90+9×80+4×70)=87.6(分),
(11×100+1×90+9×80+4×70)=87.6(分),
c=100(分)
(3)解:从平均数看,两班的成绩一样,但从中位数看,一班的中位数为90分,二班的中位数为80分,则二班比一班成绩好
【解析】(1)用样本容量分别减去一班中A、B、D等级的人数得到C等级的人数,然后补全一班竞赛成绩统计图;(2)先利用扇形统计图计算出二班中各等级的人数,然后利用众数、中位数和平均数的定义计算a、b、c、d的值;(3)利用平均数和中位数的意义求解.
【考点精析】掌握统计表是解答本题的根本,需要知道制作统计表的步骤:(1)收集整理数据.(2)确定统计表的格式和栏目数量,根据纸张大小制成表格.(3)填写栏目、各项目名称及数据.(4)计算总计和合计并填入表中,一般总计放在横栏最左格,合计放在竖栏最上格.(5)写好表格名称并标明制表时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的个数是( )
①0是最小的整数; ②一个有理数,不是正数就是负数;
③a是正数,-a是负数; ④自然数一定是正数;
⑤非正数就是负数和0.
A. 0B. 1C. 2D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列解答中,填写适当的理由或数学式:

(1)∵ ∠ABD=∠CDB, ( 已知 )
∴ ∥ . ( )
(2)∵ ∠ADC+∠DCB=180°, ( 已知 )
∴ ∥ . ( )
(3)∵ AD∥BE, ( 已知 )
∴ ∠DCE=∠ . ( )
(4)∵ ∥ , ( 已知 )
∴ ∠BAE=∠CFE. ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图12,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与CF平行吗?请说明理由;
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
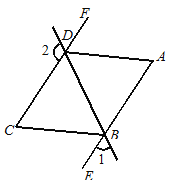
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:
(1)AE∥CF,理由如下:
∵ ∠CDB+∠2=180°, ( 平角的定义 )
∠1+∠2=180°, ( 已知 )
∴ ∠1=∠ , ( )
∴ AE∥CF. ( )
(2)AD与BC的位置关系是: .
∵ AE∥CF,( 已知 )
∴ ∠C=∠ .( )
又∵ ∠A=∠C,( 已知 )
∴ ∠A=∠CBE . ( )
∴ ∥ .( )
(3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=2x-3平移,使之经过点(1,4),则平移后的直线是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车司机国庆节的营运全是在长虹路南北方向上进行的,如果规定向北为正,向南为负,他这天行车里程(单位:千米)如下:
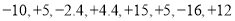
(1) 最后一名乘客送到目的地时,出租车在出发点的哪个方向?与出发点的距离?
(2) 长虹路南北至少有多少千米?
(3) 若该出租车耗油量为每千米0.08升,每升油7.5元,出租车按物价部门规定,起步价(不超过3千米)5元,超过3千米的部分,每千米(不足1千米按1千米计算)加价2元,该出租车司机今天的纯收入为多少元?(纯收入=收入-油耗钱)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数
 (k>0,x>0)的图象上,点D的坐标为(
(k>0,x>0)的图象上,点D的坐标为( ,2).
,2).(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的一个顶点恰好落在函数
 (k>0,x>0)的图象上时,求菱形ABCD平移的距离;
(k>0,x>0)的图象上时,求菱形ABCD平移的距离;
相关试题

