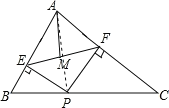
【题目】如图,在![]() ABC中,AB=5,AC=12,BC=13,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )
ABC中,AB=5,AC=12,BC=13,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】B
【解析】
先求证四边形AFPE是矩形,再根据直线外一点到直线上任一点的距离,垂线段最短,利用面积法可求得AP最短时的长,然后即可求出AM最短时的长.
解:连接AP,在![]() ABC中,AB=5,AC=12,BC=13,
ABC中,AB=5,AC=12,BC=13,
∴AB2+AC2=BC2,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP.
∵M是EF的中点,
∴AM=![]() AP,
AP,
根据直线外一点到直线上任一点的距离,垂线段最短,
即AP⊥BC时,AP最短,同样AM也最短,
∴S△ABC=![]() ,
,
∴![]() ,
,
∴AP最短时,AP=![]() ,
,
∴当AM最短时,AM=![]() AP=
AP=![]() .
.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,∠ABE=
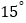 ,且AB=AE,则DE的长度为( )
,且AB=AE,则DE的长度为( )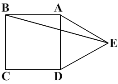
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐红萝卜,以每筐25千克为标准,超过记正不足记负来表示,记录如下:

(1)20筐红萝卜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准质量比较,20筐红萝卜总计超过或不足多少千克?
(3)若该种红萝卜进价每千克为1.5元,售价每千克为3元.求这20筐红萝卜能赚多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】 ①如图(1),直线l上有2个点,则图中有2条可用图中字母表示的射线,有1条线段
 ;
;②如图(2),直线l上有3个点,则图中有 条可用图中字母表示的射线,有 条线段;
③如图(3),直线l上有n个点,则图中有 条可用图中字母表示的射线,有 条线段;
④应用(3)中发现的规律解决问题:某校七年级共有8个班进行足球比赛,准备进行循环赛(即每两队之间赛一场),预计全部赛完共需 场比赛.
-
科目: 来源: 题型:
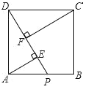
查看答案和解析>>【题目】如图,在正方形ABCD中,点P在AB边上,AE⊥DP于E点,CF⊥DP于F点,若AE=5,CF=9,则EF=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sin α=
 ,求sin 2α的值.
,求sin 2α的值.小娟是这样给小芸讲解的:
如图①,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°. 设∠BAC=α,则sin α=
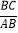 =
= .易得∠BOC=2α.设BC=x,则AB=3x,AC=2
.易得∠BOC=2α.设BC=x,则AB=3x,AC=2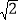 x.作CD⊥AB于D,求出CD=________(用含x的式子表示),可求得sin 2α=
x.作CD⊥AB于D,求出CD=________(用含x的式子表示),可求得sin 2α=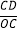 =________.
=________.【问题解决】已知,如图②,点M,N,P为⊙O上的三点,且∠P=β,sin β=
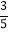 ,求sin 2β的值.
,求sin 2β的值.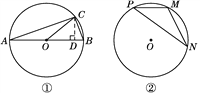
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
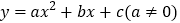 的顶点坐标为
的顶点坐标为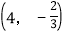 ,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
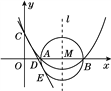
,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
相关试题

