【题目】小华骑自行车上学,当他骑了一段路时,想起要买本书,于是又这回到刚经过的某书店,买到书后继续去学校,以下是他本次上学所用的时间与离家距离的关系示意图.根据图中提供的信息回答下列问题: 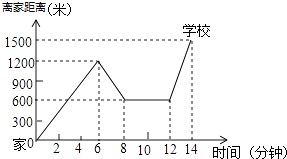
(1)小华家到学校的路程是m,小华在书店停留了min.
(2)在整个上学的途中哪个时间段小华的骑车速度最快?最快的速度是多少?
(3)本次上学途中,小华一共骑行了多少米?
(4)如果小华到校后立刻以300m/min的速度回家,请在原图上画出小华回家所用时间与离家距离的关系图象.
参考答案:
【答案】
(1)1500;4
(2)解:从开始到6分钟的速度是 ![]() =200m/min,
=200m/min,
从6分钟到8分钟的速度是: ![]() =300m/min;
=300m/min;
从12分钟到14分钟的速度是: ![]() =450m/min.
=450m/min.
则从12分钟到14分钟的速度最快,速度是450m/min
(3)解:小华一共骑行的路程是:1200+600+(1500﹣600)=2700(min)
(4)解:小华回家的时间是 ![]() =5(min)
=5(min)

【解析】解:(1)小华到学校的路程是1500m,在书店停留的时间是12﹣8=4(min). 故答案是:1500,4;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂为了解工人在单位时间内加工同一种零件的技能水平,随机从50名工人加工的零件中各抽取了10个进行检测,统计出他们各自加工的合格品数是1到8这八个整数,现提供的部分信息如图.

请解答下列问题:
(1)根据上述信息,写出这50名工人加工出合格品数的众数;
(2)求这50名工人加工出的合格品数的中位数;
(3)厂方认定,工人在单位时间内加工出的合格品数不低于3件(含3件)为技能合格,否则,将接受技能再培训.已知该厂有同类工人400名,请估计该厂将接受技能再培训的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“一个三角形中至多有一个钝角”时,应假设 .
-
科目: 来源: 题型:
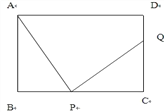
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动。设点P的运动时间为t秒,当点P从点B开始运动,同时,点Q从点C出发,沿CD向点D运动,当t =________秒时,以P、C、Q为顶点的三角形与△ABP全等。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为抑制高房价,照顾低收入家庭,国家决定加大经济保障房建设力度,若某市2017年完成了500万套,计划2019年完成2000万套.则2017年至2019年经济保障房平均每年的增长率为_____.
-
科目: 来源: 题型:
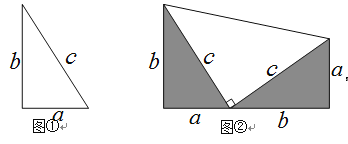
查看答案和解析>>【题目】(10分)图②是一个直角梯形.该图案可以看作由2个边长为a、b、c的直角三角形(图①)和1个腰长为c的等腰直角三角形拼成。
(1)根据图②和梯形面积的不同计算方法,可以验证一个含a、b、c的等式,请你写出这个等式,并写出其推导过程;
(2)若直角三角形的边长a、b、c满足条件:a―b=1, ab=4.试求出c的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数.

相关试题

