【题目】如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15). 
(1)当t为何值时,射线OC与OD重合;
(2)当t为何值时,射线OC⊥OD;
(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.
参考答案:
【答案】
(1)解:由题意可得,
20t=5t+120
解得t=8,
即t=8min时,射线OC与OD重合
(2)解:由题意得,
20t+90=120+5t或20t﹣90=120+5t,
解得,t=2或t=14
即当t=2min或t=14min时,射线OC⊥OD
(3)解:存在,
由题意得,120﹣20t=5t或20t﹣120=5t+120﹣20t或20t﹣120﹣5t=5t,
解得t=4.8或t= ![]() 或t=12,
或t=12,
即当以OB为角平分线时,t的值为4.8min;当以OC为角平分线时,t的值为 ![]() min,当以OD为角平分线时,t的值为12min
min,当以OD为角平分线时,t的值为12min
【解析】(1)根据题意可得,射线OC与OD重合时,20t=5t+120,可得t的值;(2)根据题意可得,射线OC⊥OD时,20t+90=120+5t或20t﹣90=120+5t,可得t的值;(3)分三种情况,一种是以OB为角平分线,一种是以OC为角平分线,一种是以OD为角平分线,然后分别进行讨论即可解答本题.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对角的运算的理解,了解角之间可以进行加减运算;一个角可以用其他角的和或差来表示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断对错:关于中心对称的两个图形全等;_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】“如果a>b,那么ac>bc”是真命题还是假命题?如果是假命题,举一个反例并添加适当的条件使它成为真命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△
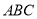 和△
和△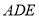 都是等腰直角三角形,
都是等腰直角三角形, 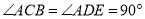 ,
, 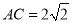 ,
, 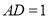 ,
, 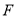 是
是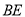 的中点.若将△
的中点.若将△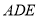 绕点
绕点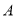 旋转一周,则线段
旋转一周,则线段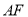 长度的取值范围是( )
长度的取值范围是( )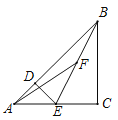
A.
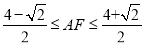 B.
B. 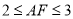
C.
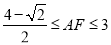 D.
D. 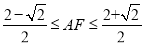
-
科目: 来源: 题型:
查看答案和解析>>【题目】倒数是它本身的数是( )
A. 1 B. ﹣1 C. 1或﹣1 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个锐角的和不可能是( )
A.锐角 B.直角 C.钝角 D.平角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是半径为
是半径为 的⊙
的⊙ 的直径,
的直径, 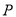 是圆上异于
是圆上异于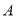 ,
,  的任意一点,
的任意一点,  的平分线交⊙
的平分线交⊙ 于点
于点 ,连接
,连接 和
和 ,△
,△ 的中位线所在的直线与⊙
的中位线所在的直线与⊙ 相交于点
相交于点 、
、 ,则
,则 的长是____.
的长是____. 
相关试题

