【题目】平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点 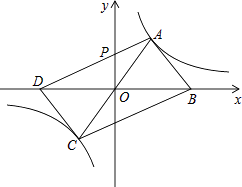
(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)在(1)的条件下,若△APO的面积为2,求点D到直线AC的距离.
参考答案:
【答案】
(1)解:∵点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,
∴3= ![]() ,点C与点A关于原点O对称,
,点C与点A关于原点O对称,
∴k=6,C(﹣2,﹣3),
即k的值是6,C点的坐标是(﹣2,﹣3);
(2)解:过点A作AN⊥y轴于点N,过点D作DM⊥AC,如图,
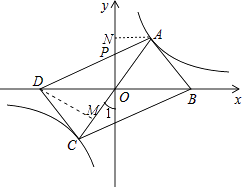
∵点A(2,3),k=6,
∴AN=2,
∵△APO的面积为2,
∴ ![]() ,
,
即 ![]() ,得OP=2,
,得OP=2,
∴点P(0,2),
设过点A(2,3),P(0,2)的直线解析式为y=kx+b,
![]() ,得
,得 ![]() ,
,
∴过点A(2,3),P(0,2)的直线解析式为y=0.5x+2,
当y=0时,0=0.5x+2,得x=﹣4,
∴点D的坐标为(﹣4,0),
设过点A(2,3),B(﹣2,﹣3)的直线解析式为y=mx+b,
则 ![]() ,得
,得 ![]() ,
,
∴过点A(2,3),C(﹣2,﹣3)的直线解析式为y=1.5x,
∴点D到直线AC的直线得距离为: ![]() =
= ![]() .
.
【解析】(1)根据点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据点到直线的距离公式可以求得点D到直线AC的距离.
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据点到直线的距离公式可以求得点D到直线AC的距离.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计划拨款9万元从厂家购进50台电视机
 已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元. 若商场同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下商场的进货方案;
若商场同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下商场的进货方案; 若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元
若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元 在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案;
在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案; 若商场准备用9万元同时购进三种不同的电视机50台,请你设计进货方案.
若商场准备用9万元同时购进三种不同的电视机50台,请你设计进货方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】长江是我们的母亲河,金港新区为了打造沿江风景,吸引游客搞活经济,将一段长为180米的沿江河道整治任务交由A、B两工程队先后接力完成.A工作队每天整治12米,B工程队每天整治8米,共用时20天.求A、B两工程队分别整治河道多少米?
⑴根据题意,七⑴班甲同学列出尚不完整的方程组如下。根据甲同学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全甲同学所列的方程组;
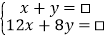 ,x表示________________________,y表示_________________________;
,x表示________________________,y表示_________________________;⑵如果乙同学直接设A工程队整治河道的米数为x,B工程队整治河道的米数为y,列出了一个方程组,求A、B两工程队分别整治河道多少米.请你帮助他写出完整的解答过程。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某品牌电风扇销售量的情况,对某商场5月份该品牌甲、乙、丙三种型号的电风扇销售量进行统计,绘制如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该商场5月份售出这种品牌的电风扇共多少台?
(2)若该商场计划订购这三种型号的电风扇共2000台,根据5月份销售量的情况,求该商场应订购丙种型号电风扇多少台比较合理?

-
科目: 来源: 题型:
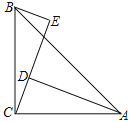
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D、E
(1) 求证:CD=BE
(2) 若AD=3.5 cm,DE=2.7 cm,求BE的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,E为AC上一点,∠ABE=∠AEB,∠CDE=∠CED.
求证:BE⊥DE.

相关试题

