【题目】已知![]() ,
,![]() .
.
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 的值比
的值比![]() 的值的
的值的![]() 大1;
大1;
(3)先填表,后回答:
|
|
|
| 0 | 1 | 2 | 3 | 4 |
| ||||||||
|
根据所填表格,回答问题:随着![]() 值的增大,
值的增大,![]() 的值逐渐 ;
的值逐渐 ;![]() 的值逐渐 .
的值逐渐 .
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)表格详见解析,减小,增大.
;(3)表格详见解析,减小,增大.
【解析】
(1)由题意可得关于x的方程,解方程即得答案;
(2)根据![]() =
=![]()
![]() +1可得关于x的方程,解方程即得答案;
+1可得关于x的方程,解方程即得答案;
(3)把x的值依次代入![]() 和
和![]() 的关系式进行计算,即可完成表格;根据所填表格中的数据即可判断
的关系式进行计算,即可完成表格;根据所填表格中的数据即可判断![]() 和
和![]() 的变化趋势.
的变化趋势.
解:(1)由题意得:![]() ,解得:
,解得:![]() ,
,
所以,当![]() 时,
时,![]() ;
;
(2)由题意得: ![]() ,解得:
,解得:![]() ,
,
所以,当![]() 时,
时,![]() 的值比
的值比![]() 的值的
的值的![]() 大1.
大1.
(3)
|
|
|
| 0 | 1 | 2 | 3 | 4 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|
|
|
|
| 0 | 2 | 4 | 6 |
由表格中的数据可知:随着![]() 值的增大,
值的增大,![]() 的值逐渐减小;
的值逐渐减小;![]() 的值逐渐增大.
的值逐渐增大.
故答案为:减小,增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为4的正方形ABCD,顶点A与坐标原点重合,一反比例函数图象过顶点C,动点P以每秒1个单位速度从点A出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC﹣CB﹣BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
(1)求出该反比例函数解析式;
(2)连接PD,当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时,求点Q的坐标;
(3)用含t的代数式表示以点Q、P、D为顶点的三角形的面积s,并指出相应t的取值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情況记录如下(单位:
 ):
):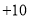 ,
,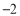 ,
,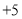 ,
,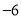 ,
,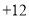 ,
,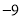 ,
,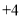 ,
,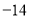 .(假定开始计时时,守门员正好在球门线上)
.(假定开始计时时,守门员正好在球门线上)(1)守门员最后是否回到球门线上?
(2)守门员在这段时间内共跑了多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为15,OC边长为3.

(1)数轴上点A表示的数为 .
(2)将长方形OABC沿数轴水平方向移动,移动后的长方形记为O′A′B′C′(O、A、B、C对应点分别为O′、A′、B′、C′),移动后的长方形O′A′B′C′与原长方形OABC重叠部分的周长记为L.
①当L=10时,移动的距离为 ;
②当L恰好等于原长方形OABC周长的一半时,数轴上点A′表示的数为 .
③设点A的移动距离AA′=x.若D为线段AA′的中点,点E在线段OO′上,且OE=
 OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1 cm,△ACD的周长为12 cm,则△ABC的周长是( )

A. 13 cm B. 14 cm C. 15 cm D. 16 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
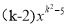 为反比例函数.
为反比例函数.(1)求k的值;
(2)它的图象在第 象限内,在各象限内,y随x增大而 ;(填变化情况)
(3)求出﹣2≤x≤﹣
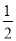 时,y的取值范围.
时,y的取值范围.
相关试题

