搜索
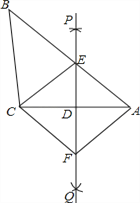
【题目】如图，在△ABC中， PQ是CA的垂直平分线， CF∥AB交PQ于点F，连接AF．
（1）求证：△AED≌△CFD；
（2）求证：四边形AECF是菱形．
参考答案：
【答案】（1）证明见解析；（2）证明见解析
【解析】试题分析：（1）本题利用平行线的性质得出角相等，再利用垂直平分线的性质得出线段相等，从而得出全等三角形即可；（2）由全等三角形得出AE=CF,得出四边形AECF是平行四边形，DE=DF,得出四边形AECF是菱形．
试题解析：
（1）PQ为线段AC的垂直平分线，
∴AE=CE，AD=CD，
∵CF∥AB
∴∠EAC=∠FCA，∠CFD=∠AED，
在△AED与△CFD中，
，
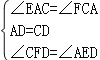∴△AED≌△CFD；
（2）∵△AED≌△CFD，
∴AE=CF，
∵EF为线段AC的垂直平分线，
∴EC=EA，FC=FA，
∴EC=EA=FC=FA，
∴四边形AECF为菱形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形网格中，每个小正方形的边长为1个单位长度．平面直角坐标系xOy的原点O在格点上，x轴、y轴都在格线上．线段AB的两个端点也在格点上．
（1）若将线段AB绕点O逆时针旋转90°得到线段A1B1，试在图中画出线段A1B1．
（2）若线段A2B2与线段A1B1关于y轴对称，请画出线段A2B2．
（3）若点P是此平面直角坐标系内的一点，当点A、B1、B2、P四边围成的四边形为平行四边形时，请你直接写出点P的坐标(写出一个即可)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市某学校开展“远是君山，磨砺意志，保护江豚，爱鸟护鸟”为主题的远足活动．已知学校与君山岛相距24千米，远足服务人员骑自行车，学生步行，服务人员骑自行车的平均速度是学生步行平均速度的2.5倍，服务人员与学生同时从学校出发，到达君山岛时，服务人员所花时间比学生少用了3.6小时，求学生步行的平均速度是多少千米/小时．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，直线y=
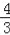x+4交于x轴于点A，交y轴于点C，过A、C两点的抛物线F1交x轴于另一点B（1，0）．（1）求抛物线F1所表示的二次函数的表达式；
（2）若点M是抛物线F1位于第二象限图象上的一点，设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC，记S=S四边形MAOC﹣S△BOC，求S最大时点M的坐标及S的最大值；
（3）如图②，将抛物线F1沿y轴翻折并“复制”得到抛物线F2，点A、B与（2）中所求的点M的对应点分别为A′、B′、M′，过点M′作M′E⊥x轴于点E，交直线A′C于点D，在x轴上是否存在点P，使得以A′、D、P为顶点的三角形与△AB′C相似？若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】两名同学在调查时使用下面两种提问方式,你认为哪一种更好些( )
A. 难道你不认为科幻片比武打片更有意思吗?
B. 你更喜欢哪一类电影 ——科幻片还是武打片?
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知两组数据：a1，a2，a3，a4，a5和a1-1，a2-1，a3-1，a4-1，a5-1，下列判断中错误的是（ ）
A. 平均数不相等，方差相等 B. 中位数不相等，标准差相等
C. 平均数相等，标准差不相等 D. 中位数不相等，方差相等
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学活动﹣旋转变换
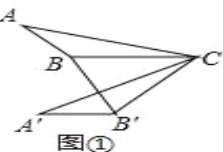
（1）如图①，在△ABC中，∠ABC=130°，将△ABC绕点C逆时针旋转50°得到△A′B′C，连接BB′，求∠A′B′B的大小；
（2）如图②，在△ABC中，∠ABC=150°，AB=3，BC=5，将△ABC绕点C逆时针旋转60°得到△A′B′C，连接BB′，以A′为圆心，A′B′长为半径作圆．
（Ⅰ）猜想：直线BB′与⊙A′的位置关系，并证明你的结论；
（Ⅱ）连接A′B，求线段A′B的长度；
（3）如图③，在△ABC中，∠ABC=α（90°＜α＜180°），AB=m，BC=n，将△ABC绕点C逆时针旋转2β角度（0°＜2β＜180°）得到△A′B′C，连接A′B和BB′，以A′为圆心，A′B′长为半径作圆，问：角α与角β满足什么条件时，直线BB′与⊙A′相切，请说明理由，并求此条件下线段A′B的长度（结果用角α或角β的三角函数及字母m、n所组成的式子表示）
相关试题
