【题目】如图,在等边三角形ABC中,点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,AD、BE相交于F点. 
(1)求证:△ABE≌△CAD;
(2)当E、D运动时,∠BFD大小是否发生改变?若不变求其大小,若改变求其变化范围.
参考答案:
【答案】
(1)解:∵△ABC是等边三角形,
∴AC=AB,∠C=∠BAE=60°,
∵点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,
∴BD=CE,
∴AE=CD,
在△ABE和△CAD中,
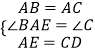 ,
,
∴△ABE≌△CAD
(2)解:当E、D运动时,∠BFD大小不发生改变,
∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∵∠AFE=∠ABE+∠BAF,
∴∠AFE=∠CAD+∠BAF=∠BAC=60°,
∵∠AFE=∠BFD(对顶角相等),
∴∠BFD=60°
【解析】(1)由等边三角形ABC可得出的条件是:AB=AC,∠BAC=∠ACB=60°,可根据SAS证明△ABE≌△CAD;(2)E、D运动时,∠BFD大小不发生改变,根据△ABE≌△CAD,得到∠ABE=∠CAD,利用外角的性质得到∠AFE=∠ABE+∠BAF,再根据对顶角相等,即可解答.
【考点精析】根据题目的已知条件,利用等边三角形的性质的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式3x2+5x的值为5,则代数式10x﹣9+6x2的值是( )
A. ﹣1B. 1C. 5D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是随机事件的是( )
A.任意画两个直角三角形,这两个三角形相似B.相似三角形的对应角相等
C.⊙O的半径为5,OP=3,点P在⊙O外D.直径所对的圆周角为直角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
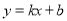 与反比例函数
与反比例函数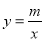 交于A(1,﹣3),B(a,﹣1)两点.
交于A(1,﹣3),B(a,﹣1)两点.(1)求一次函数的解析式;
(2)根据反比例函数
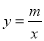 的图象,当y>6时,求出x的取值范围;
的图象,当y>6时,求出x的取值范围;(3)若一次函数
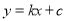 与反比例函数
与反比例函数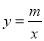 有一个交点,求c的值.
有一个交点,求c的值.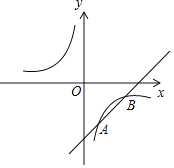
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形的外角和是________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在△ABC中,∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6
求BC的长.
小聪思考:因为CD平分∠ACB,所以可在BC边上取点E,使EC=AC,连接DE.这样很容易得到△DEC≌△DAC,经过推理能使问题得到解决(如图2).
请回答:
(1)△BDE是
(2)BC的长为
相关试题

