【题目】如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
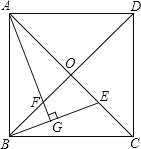
(1)试说明OE=OF;
(2)当AE=AB时,过点E作EH⊥BE交AD边于H,找出与△AHE全等的一个三角形加以证明,
(3)在(2)的条件下若该正方形边长为1,求AH的长.
参考答案:
【答案】(1)证明解解析(2)答案见解析(3)![]() ﹣1
﹣1
【解析】
试题分析:(1)根据正方形性质得出AC⊥BD,OA=OB,求出∠FAO=∠EBO,根据ASA推出△AFO≌△BEO即可;
(2)根据正方形性质得出∠ACB=∠DAC=45°,∠ABE+∠EBC=90°,求出∠CBE=∠AEH,AE=AB=BC,证△BCE≌△EAH;
(3)根据全等三角形的性质推出CE=AH,即可得出答案.
(1)解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OB,
∴∠AOF=∠BOE=90°,
∵AG⊥BE,
∴∠FGB=90°,
∴∠OBE+∠BFG=90°,∠FAO+∠AFO=90°,
∵∠AFO=∠BFG,
∴∠FAO=∠EBO,
在△AFO和△BEO中,
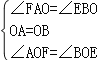 ,
,
∴△AFO≌△BEO(ASA),
∴OE=OF.

(2)△BCE≌△EAH,
证明:∵四边形ABCD是正方形,
∴∠ACB=∠DAC=45°,∠ABE+∠EBC=90°,
∵EH⊥BE,
∴∠AEH+∠AEB=90°,
∵AE=AB,
∴∠ABE=∠AEB,
∴∠CBE=∠AEH,
∵AE=AB=BC,
在△BCE和△EAH中,
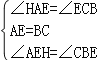 ,
,
∴△BCE≌△EAH(ASA);
(3)解:∵△BCE≌△EAH,
∴CE=AH,
∵AB=BC=1,
∴AC=![]() ,
,
∵AE=AB=1,
∴AH=CE=AC﹣AE=![]() ﹣1.
﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式2x2+3x+7的值为8,则代数式4x2+6x-9的值是( )
A. 13 B. 2 C. 17 D. -7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
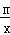 的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,﹣2).
的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,﹣2).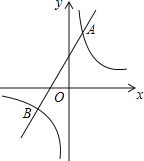
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10
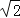 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据:
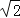 ≈1.41,
≈1.41,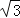 ≈1.73,
≈1.73,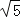 ≈2.24)
≈2.24)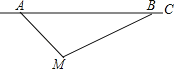
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c=(a≠0)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②b2﹣4ac>0;③9a﹣3b+c<0;④b﹣4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=﹣4,其中正确的结论有( )
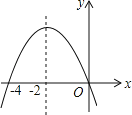
A.①③④ B.②④⑤ C.①②⑤ D.②③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】“铁路建设助推经济发展”,近年来我国政府十分重视铁路建设.渝利铁路通车后,从重庆到上海比原铁路全程缩短了320千米,列车设计运行时速比原铁路设计运行时速提高了l20千米/小时,全程设计运行时间只需8小时,比原铁路设计运行时间少用16小时.
(1)渝利铁路通车后,重庆到上海的列车设计运行里程是多少千米?
(2)专家建议:从安全的角度考虑,实际运行时速要比设计时速减少m%,以便于有充分时间应对突发事件,这样,从重庆到上海的实际运行时间将增加
 m小时,求m的值.
m小时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国的国土面积为9596950平方千米,按四舍五入保留三个有效数字,则我国的国土面积可表示为________平方千米。
相关试题

