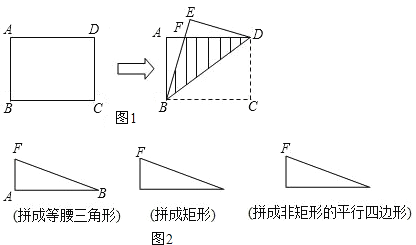
【题目】已知:如图1,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分(△BFD)剪去,得到△ABF和△EDF.
(1)求证:FB=FD;
(2)求证:△ABF≌△EDF;
(3)将△ABF与△EDF不重合地拼在一起,可拼成特殊三角形和特殊四边形,请你按照下列要求将拼图补画完整(图2).
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】(1)根据翻折的性质得出∠FBD=∠DBC,再利用平行线的性质证明即可;
(2)由折叠的性质求证△ABF≌△EFD;
(3)根据题意要求作图即可.
(1)证明:由折叠的性质知,∠FBD=∠DBC,
∵矩形ABCD,
∴AD∥BC,
∴∠FDB=∠DBC,
∴∠FBD=∠FDB,
∴FB=FD;
(2)证明:由折叠的性质知,ED=CD=AB,
又∵∠E=∠A=90°,∠EFD=∠AFB,
∴△ABF≌△EFD;
(3)如图,
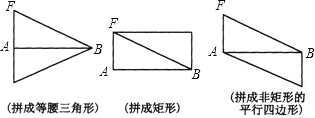
-
科目: 来源: 题型:
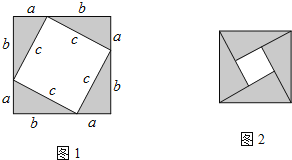
查看答案和解析>>【题目】阅读下面的材料:勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到(a+b)2=4×
 ab+c2
ab+c2整理,得a2+2ab+b2=2ab+c2.
所以a2+b2=c2.
如果把图1中的四个全等的直角三角形摆成图2所示的正方形,请你参照上述方法证明勾股定理.
-
科目: 来源: 题型:
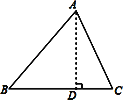
查看答案和解析>>【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路:

(1)请你按照他们的解题思路过程完成解答过程;
(2)填空:在△DEF中,DE=15,EF=13,DF=4,则△DEF的面积是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一些数排列成下表中的四列:
第1列
第2列
第3列
第4列
第1行
1
4
5
10
第2行
4
8
10
12
第3行
9
12
15
14
…
…
…
…
…
(1)第4行第1列的数是多少?直接写出答案;
(2)第17行的四个数之和是多少?请写出适当的过程;
(3)数100所在的行和列分别是多少?直接写出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有A、B、C三点,点A和点B所表示的数分别为﹣3和+
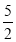 ,点C到点A、点B的距离相等.
,点C到点A、点B的距离相等.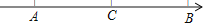
(1)点C表示的数为 ;
(2)若数轴上有一点P,若满足PA+PB=10,求点P表示的数;
(3)若数轴上有一点Q.若满足QA+QB﹣QC=
 ,求点Q表示的数.
,求点Q表示的数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴表示的是5个城市的国际标准时间(单位:时),如果北京的时间是2020年1月9日上午9时,下列说法正确的是( )

A.伦敦的时间是2020年1月9日凌晨1时
B.纽约的时间是2020年1月9日晚上20时
C.多伦多的时间是2020年1月8日晚上19时
D.汉城的时间是2020年1月9日上午8时
相关试题

