【题目】将一些数排列成下表中的四列:
第1列 | 第2列 | 第3列 | 第4列 | |
第1行 | 1 | 4 | 5 | 10 |
第2行 | 4 | 8 | 10 | 12 |
第3行 | 9 | 12 | 15 | 14 |
… | … | … | … | … |
(1)第4行第1列的数是多少?直接写出答案;
(2)第17行的四个数之和是多少?请写出适当的过程;
(3)数100所在的行和列分别是多少?直接写出答案.
参考答案:
【答案】(1)16;(2)484;(3) 数100在第10行第1列,第25行第2列,第20行第3列,第46行第4列.
【解析】
(1)观察可知,第1列的数从上往下依次为![]() ,
,![]() ,
,![]() ,
,![]() ,可得第4行第1列的数;
,可得第4行第1列的数;
(2)第1列的数的数为![]() ,第2列的数为
,第2列的数为![]() ,第3列的数为
,第3列的数为![]() ,第4列为
,第4列为![]() ,相加即可得到结论;
,相加即可得到结论;
(3)第3列的数从上往下依次为![]() ,
,![]() ,
,![]() ,
,![]() ;第4列的数从上往下依次为
;第4列的数从上往下依次为![]() ,
,![]() ,
,![]() ,
,![]() ,根据各列的变化规律可得100所在的行和列.
,根据各列的变化规律可得100所在的行和列.
解:(1)根据表格中的规律,第一列的数分别为1,4,9,…,分别为12,22,32,…,
∴第4行第1列的数是42=16;
(2)∵第17行第1列的数的数为172,第17行第2列的数为4×17,第17行第3列的数为5×17,第17行第4列为10+2(17﹣1),
∴第17行的四个数之和是172+4×17+5×17+10+2(17﹣1)=484;
(3)∵100=102,
∴数100在第10行第1列;
∵100=4×25,
∴数100在第25行第2列;
∵100=5×20,
∴数100在第20行第3列;
∵100=50×2=(46+4)×2,
∴数100在第46行第4列.
综上所述,数100在第10行第1列,第25行第2列,第20行第3列,第46行第4列.
-
科目: 来源: 题型:
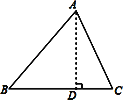
查看答案和解析>>【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路:

(1)请你按照他们的解题思路过程完成解答过程;
(2)填空:在△DEF中,DE=15,EF=13,DF=4,则△DEF的面积是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

-
科目: 来源: 题型:
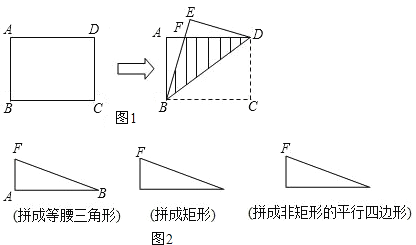
查看答案和解析>>【题目】已知:如图1,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分(△BFD)剪去,得到△ABF和△EDF.
(1)求证:FB=FD;
(2)求证:△ABF≌△EDF;
(3)将△ABF与△EDF不重合地拼在一起,可拼成特殊三角形和特殊四边形,请你按照下列要求将拼图补画完整(图2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有A、B、C三点,点A和点B所表示的数分别为﹣3和+
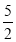 ,点C到点A、点B的距离相等.
,点C到点A、点B的距离相等.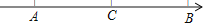
(1)点C表示的数为 ;
(2)若数轴上有一点P,若满足PA+PB=10,求点P表示的数;
(3)若数轴上有一点Q.若满足QA+QB﹣QC=
 ,求点Q表示的数.
,求点Q表示的数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴表示的是5个城市的国际标准时间(单位:时),如果北京的时间是2020年1月9日上午9时,下列说法正确的是( )

A.伦敦的时间是2020年1月9日凌晨1时
B.纽约的时间是2020年1月9日晚上20时
C.多伦多的时间是2020年1月8日晚上19时
D.汉城的时间是2020年1月9日上午8时
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图(1),
 ,
,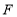 ,
, ,
, 四点分别在四边形
四点分别在四边形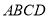 的四条边上,若四边形
的四条边上,若四边形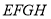 为菱形,我们称菱形
为菱形,我们称菱形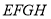 为四边形
为四边形 的内接菱形.
的内接菱形.动手操作:

(1)如图2,网格中的每个小四边形都为正方形,每个小四边形的顶点叫做格点,由
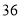 个小正方形组成一个大正方形
个小正方形组成一个大正方形 ,点
,点 、
、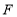 在格点上,请在图(2)中画出四边形
在格点上,请在图(2)中画出四边形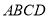 的内接菱形
的内接菱形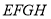 ;
;特例探索:
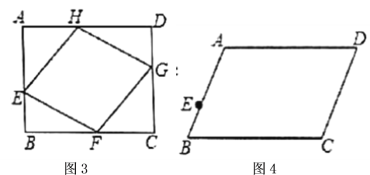
(2)如图3,矩形
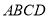 ,
, ,点
,点 在线段
在线段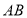 上且
上且 ,四边形
,四边形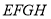 是矩形
是矩形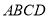 的内接菱形,求
的内接菱形,求 的长度;
的长度;拓展应用:
(3)如图4,平行四边形
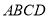 ,
, ,
, ,点
,点 在线段
在线段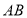 上且
上且 ,
,①请你在图4中画出平行四边形
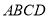 的内接菱形
的内接菱形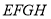 ,点
,点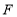 在边
在边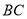 上;
上;②在①的条件下,当
 的长最短时,
的长最短时,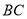 的长为__________
的长为__________
相关试题

