【题目】如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( ) 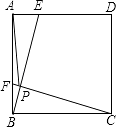
A.2
B.2 ![]()
C.4 ![]() ﹣2
﹣2
D.2 ![]() ﹣2
﹣2
参考答案:
【答案】D
【解析】解:在正方形ABCD中,
∴AB=BC,∠BAE=∠ABC=90°,
在△ABE和△BCF中,
∵ 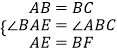 ,
,
∴△ABE≌△BCF(SAS),
∴∠ABE=∠BCF,
∵∠ABE+∠CBP=90°
∴∠BCF+∠CBP=90°
∴∠BPC=90°
如图,取BC的中点O,连接OP、OA,
则OP= ![]() BC=2,
BC=2,
在Rt△AOB中,OA= ![]() =
= ![]() =2
=2 ![]() ,
,
根据三角形的三边关系,OP+AP≥OA,
∴当O、P、A三点共线时,AP的长度最小,
AP的最小值=OA﹣OP=2 ![]() ﹣2.
﹣2.
故选D.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)写出图2的阴影部分的正方形的边长.
(2)用两种不同的方法求图中的阴影部分的面积.
(3)观察如图2,写出
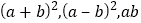 这三个代数式之间的等量关系.
这三个代数式之间的等量关系.(4)根据(3)题中的等量关系,解决问题:若
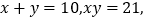 求
求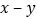 的值
的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )
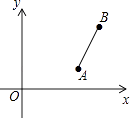
A.(1,2)
B.(2,1)
C.(7,0)
D.(1,3) -
科目: 来源: 题型:
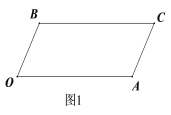
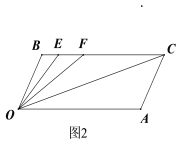
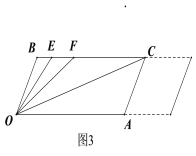
查看答案和解析>>【题目】如图1所示,已知BC∥OA, ∠B=∠A=120°.
(1)证明:OB∥AC;
(2)如图2所示,若点E,F在BC上,且∠FOC=∠AOC,OE平分∠BOF,求∠EOC的度数.
(3)在(2)的条件下,若左右平移AC,如图3所示,那么∠OCB∶∠OFB的比值是否随之发生变化?若变化,请说明理由;若不变化,请求出这个比值.
(4)在(2)和(3)的条件下,当∠OEB=∠OCA时,求∠OCA的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)
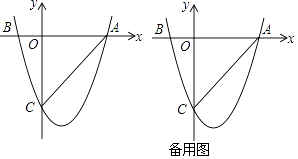
(1)求该二次函数的解析式;
(2)设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个? -
科目: 来源: 题型:
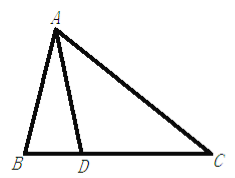
查看答案和解析>>【题目】如图,在△ABC中,AB=AD=DC,∠BAD=32°,则∠C=________.
相关试题

