【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)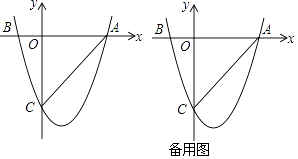
(1)求该二次函数的解析式;
(2)设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个?
参考答案:
【答案】
(1)解:设抛物线解析式为y=a(x+1)(x﹣3),
把C(0,﹣3)代入得﹣3a=﹣3,解得a=1,
所以抛物线解析式为y=(x+1)(x﹣3),
即y=x2﹣2x﹣3
(2)解:抛物线的对称轴为直线x=1,
设E(t,t2﹣2t﹣3),
当0<t<1时,如图1,
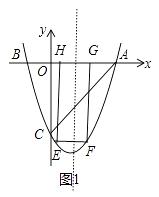
EF=2(1﹣t),EH=﹣(t2﹣2t﹣3),
∵矩形EFGH为正方形,
∴EF=EH,即2(1﹣t)=﹣(t2﹣2t﹣3),
整理得t2﹣4t﹣1=0,解得t1=2+ ![]() (舍去),t2=2﹣
(舍去),t2=2﹣ ![]() (舍去);
(舍去);
当1<t<3时,如图2,
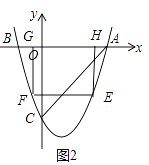
EF=2(t﹣1),EH=﹣(t2﹣2t﹣3),
∵矩形EFGH为正方形,
∴EF=EH,即2(t﹣1)=﹣(t2﹣2t﹣3),
整理得t2﹣5=0,解得t1= ![]() ,t2=﹣
,t2=﹣ ![]() (舍去),
(舍去),
此时正方形EFGH的边长为2 ![]() ﹣2;
﹣2;
当t>3时,EF=2(t﹣1),EH=t2﹣2t﹣3,
∵矩形EFGH为正方形,
∴EF=EH,即2(t﹣1)=t2﹣2t﹣3,
整理得t2﹣4t﹣1=0,解得t1=2+ ![]() ,t2=2﹣
,t2=2﹣ ![]() (舍去),
(舍去),
此时正方形EFGH的边长为2 ![]() +2,
+2,
综上所述,正方形EFGH的边长为2 ![]() ﹣2或2
﹣2或2 ![]() +2
+2
(3)解:设P(x,x2﹣2x﹣3),
当﹣1<x<0时,
∵S△ABC= ![]() ×4×3=6,
×4×3=6,
∴0<S△APC<6,
当0<x<3时,作PM∥y轴交AC于点M,如图3,
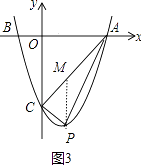
易得直线AC的解析式为y=x﹣3,则M(x,x﹣3),
∴PM=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∴S△APC= ![]() 3(﹣x2+3x)
3(﹣x2+3x)
=﹣ ![]() x2+
x2+ ![]() x
x
=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
当x= ![]() 时,S△APC的面积的最大值为
时,S△APC的面积的最大值为 ![]() ,即0<S△APC<
,即0<S△APC< ![]() ,
,
综上所述,0<S△APC<6,
∴△PAC面积为整数时,它的值为1、2、3、4、5,即△PAC有5个.
【解析】(1)设抛物线的交点式为y=a(x+1)(x﹣3),然后把C点的坐标代入即可;(2)设E(t,t2﹣2t﹣3),讨论:当0<t<1时,如图1,EF=2(1﹣t),EH=﹣(t2﹣2t﹣3),利用正方形的性质得2(1﹣t)=﹣(t2﹣2t﹣3),当1<t<3时,如图2,利用正方形的性质得2(t﹣1)=﹣(t2﹣2t﹣3),然后分别解方程得到满足条件的t的值,再计算出对应的正方形的边长;(3)设P(x,x2﹣2x﹣3),讨论:当﹣1<x<0时,由于S△ABC= 6,则0<S△APC<6,当0<x<3时,作PM∥y轴交AC于点M,如图3,求出直线AC的解析式为y=x﹣3,则M(x,x﹣3),利用三角形的面积公式得S△APC= ![]() 3(﹣x2+3x),利用二次函数的性质得0<S△APC<
3(﹣x2+3x),利用二次函数的性质得0<S△APC< ![]() ,所以0<S△APC<6,于是得到△PAC面积为整数时,它的值为1、2、3、4、5,即△PAC有5个.
,所以0<S△APC<6,于是得到△PAC面积为整数时,它的值为1、2、3、4、5,即△PAC有5个.
【考点精析】通过灵活运用确定一次函数的表达式和二次函数的性质,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.
-
科目: 来源: 题型:
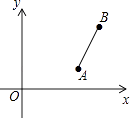
查看答案和解析>>【题目】已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )
A.(1,2)
B.(2,1)
C.(7,0)
D.(1,3) -
科目: 来源: 题型:
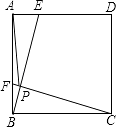
查看答案和解析>>【题目】如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )
A.2
B.2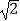
C.4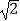 ﹣2
﹣2
D.2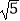 ﹣2
﹣2 -
科目: 来源: 题型:
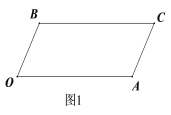
查看答案和解析>>【题目】如图1所示,已知BC∥OA, ∠B=∠A=120°.
(1)证明:OB∥AC;
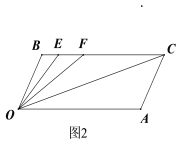
(2)如图2所示,若点E,F在BC上,且∠FOC=∠AOC,OE平分∠BOF,求∠EOC的度数.
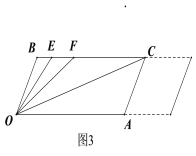
(3)在(2)的条件下,若左右平移AC,如图3所示,那么∠OCB∶∠OFB的比值是否随之发生变化?若变化,请说明理由;若不变化,请求出这个比值.
(4)在(2)和(3)的条件下,当∠OEB=∠OCA时,求∠OCA的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AD=DC,∠BAD=32°,则∠C=________.
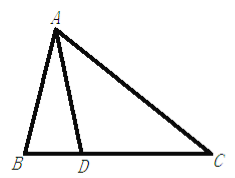
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.

(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明;
(4)若点P在C、D两点外侧运动时,请直接写出∠1、∠2、∠3之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
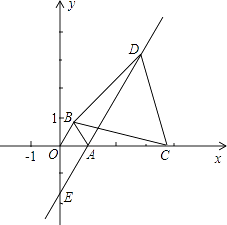
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,当点C坐标为多少时直线EF∥直线BO?这时OF和直线BO的位置关系如何?请给予证明.
相关试题

