搜索
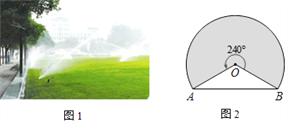
【题目】如图1是某公园一块草坪上的自动旋转喷水装置，这种旋转喷水装置的旋转角度为240°，它的喷灌区是一个扇形．小涛同学想了解这种装置能够喷灌的草坪面积，他测量出了相关数据，并画出了示意图．如图2，A，B两点的距离为18米，求这种装置能够喷灌的草坪面积．
参考答案：
【答案】72πm2.
【解析】试题分析：作OC⊥AB，根据垂径定理得出AC=9，继而可得圆的半径OA的值，再根据扇形面积公式可得答案．
试题解析：解：过点O作OC⊥AB于C点．∵OC⊥AB，AB=18，∴AC=
AB=9，∵OA=OB，∠AOB=360°﹣240°=120°，∴∠AOC=
∠AOB=60°．在Rt△OAC中，OA2=OC2+AC2 ，又∵OC=
OA，∴r=OA=
，∴S=
πr2=72π（m2）．
-
科目： 来源： 题型：
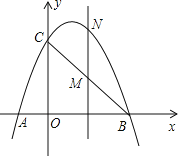
查看答案和解析>>【题目】如图，已知抛物线经过点A(－1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)点M是线段BC上的点（不与B，C重合），过M作MN∥y轴交抛物线于N若点M的横坐标为m，请用m的代数式表示MN的长。
(3)在（2）的条件下，连接NB、NC，是否存在m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】公园里有一人设了个游戏摊位，游客只需掷一枚正方体骰子，如果出现3点，就可获得价值10元的奖品，每抛掷1次骰子只需付1元的费用．小明在摊位前观察了很久，记下了游客的中奖情况：
游客
1
2
3
4
5
6
7
抛掷次数
30
20
25
6
16
50
12
中奖次数
1
0
0
1
0
2
0
看了小明的记录，你有什么看法？
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球（除颜色不同外其余都相同），其中红球有2个，黄球有1个，从中任意捧出1球是红球的概率为
．（1）试求袋中绿球的个数；
（2）第1次从袋中任意摸出1球（不放回），第2次再任意摸出1球，请你用画树状图或列表格的方法，求两次都摸到红球的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠ACB=90°，D是边AB上一点，且∠A=2∠DCB．E是BC边上的一点，以EC为直径的⊙O经过点D．
（1）求证：AB是⊙O的切线；
（2）若CD的弦心距为1，BE=EO，求BD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知数轴上点A表示的数为10， AB=16, 且B在A的左侧,动点P从点A出发，以每秒3个单位的速度沿数轴向左匀速运动，设运动时间为t(t>0）秒.
（1）写出数轴上点B表示的数_______
（2）线段AP的长为________（用含t的代数式表示）
（3）若动点Q从B出发，以每秒1个单位的速度沿数轴向右匀速运动，若P,Q同时出发，求运动多少秒时，P、Q相遇?
（4）若动点Q从B出发，以每秒1个单位的速度沿数轴向左匀速运动，若P,Q同时出发， 求点P运动多少秒时追上点Q?
-
科目： 来源： 题型：
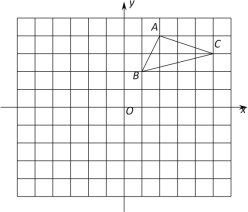
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为(2，4)．
（1）AB的长等于 ；
（2）画出△ABC向下平移5个单位后得到△A1B1C1，并写出此时点A1的坐标；
（3）画出△ABC绕原点O旋转180后得到的△A2B2C2，并写出此时点C2的坐标．
相关试题
