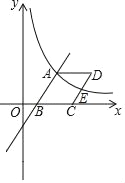
【题目】如图,已知一次函数y=![]() x﹣3与反比例函数y=
x﹣3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)求反比例函数的表达式;
(2)将线段AB沿x轴向右平移5个单位到DC,设DC与双曲线交于点E,求点E到x轴的距离.
参考答案:
【答案】(1)反比例函数的解析式为y=![]() ;(2)点E到x轴的距离为
;(2)点E到x轴的距离为![]() .
.
【解析】分析:(1)把点A(4,n)代入一次函数y=![]() x-3,得到n的值为3;再把点A(4,3)代入反比例函数y=
x-3,得到n的值为3;再把点A(4,3)代入反比例函数y=![]() ,得到k的值为12,即可写出方比例函数的解析式;
,得到k的值为12,即可写出方比例函数的解析式;
(2)设E(![]() ,m),根据tan∠ECx=tan∠ABC构建方程即可解决问题.
,m),根据tan∠ECx=tan∠ABC构建方程即可解决问题.
详解:(1)把点A(4,n)代入一次函数y=![]() x﹣3,
x﹣3,
可得n=![]() ×4﹣3=3;
×4﹣3=3;
把点A(4,3)代入反比例函数y=![]() ,
,
可得3=![]() ,
,
解得k=12.
∴反比例函数的解析式为y=![]() .
.
(2)设E(![]() ,m),
,m),
一次函数y=![]() x-3与x轴交点B(2,0),
x-3与x轴交点B(2,0),
BC=AD=5,
∴OC=7,
∵tan∠ECx=tan∠ABC,
∴![]() =
=![]() ,
,
解得m=![]() (负根已经舍弃),
(负根已经舍弃),
∴点E到x轴的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某草莓种植大户,今年从草莓上市到销售完需要20天,售价为15元/千克,成本y(元/千克)与第x天成一次函数关系,当x=10时,y=7,当x=15时,y=6.5.
(1)求成本y(元/千克)与第x天的函数关系式并写出自变量x的取值范围;
(2)求第几天每千克的利润w(元)最大?最大利润是多少?(利润=售价-成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在正方形ABCD中,点P、Q是CD边上的两点,且DP=CQ,过D作DG⊥AP于H,交AC、BC分别于E,G,AP、EQ的延长线相交于R.
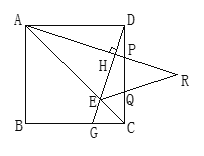
(1)求证:DP=CG;
(2)判断△PQR的形状,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了把巴城建成省级文明城市,特在每个红绿灯处设置了文明监督岗,文明劝导员老张某天在市中心的一十字路口,对闯红灯的人数进行统计.根据上午7:00~12:00中各时间段(以1小时为一个时间段),对闯红灯的人数制作了如图所示的扇形统计图和条形统计图,但均不完整.请你根据统计图解答下列问题:
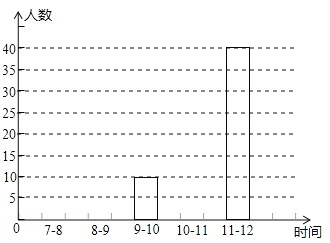

(1)问这一天上午7:00~12:00这一时间段共有多少人闯红灯?
(2)请你把条形统计图补充完整,并求出扇形统计图中9~10点,10~11点所对应的圆心角的度数.
(3)求这一天上午7:00~12:00这一时间段中,各时间段闯红灯的人数的众数和中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市在今年对全市6000名八年级学生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
组别
视力
频数(人)
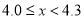
20
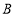
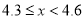
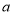
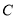
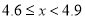
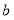
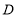
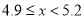
70
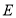
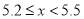
10
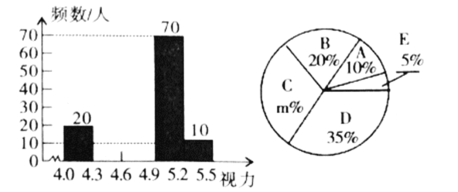
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)
 ___________,
___________,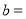 _____________,
_____________,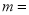 _____________;
_____________;(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是一个直角,作射线
是一个直角,作射线 ,再分别作
,再分别作 和
和 的平分线
的平分线 ,
, .
.(1)如图①,当
 时,求
时,求 的度数;
的度数;(2)如图②,当射线
 在
在 内绕
内绕 点旋转时,
点旋转时, 始终是
始终是 与
与 的平分线.则
的平分线.则 的大小是否发生变化,说明理由;
的大小是否发生变化,说明理由;(3)当射线
 在
在 外绕
外绕 点旋转且
点旋转且 为钝角时,
为钝角时, 仍始终是
仍始终是 与
与 的平分线,直接写出
的平分线,直接写出 的度数(不必写过程).
的度数(不必写过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

相关试题

