搜索
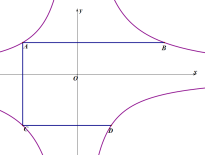
【题目】如图，A、D在反比例函数
的图像上，点B、C在反比例函数
的图像上，若AB∥CD∥
轴，
∥
轴，且
，
，
，则
=______．
参考答案：
【答案】
【解析】
过B点向x轴作垂线，交x轴于点G，过D点向x轴作垂线，交x轴于点H，根据反比例函数系数k的性质可得S矩APOM=S矩ONDH=-m，S矩PCNO=S矩MOGB=n，由此可得S矩APGB=S矩PCDH，由此即可得AP的值，再根据AP的值可得S矩APGB=n-m=4①，S矩PCNO=2S矩APOM即
②，求解即可得出n值．
解：如图，过B点向x轴作垂线，交x轴于点G，过D点向x轴作垂线，交x轴于点H，
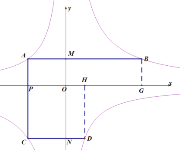
根据反比例函数系数k的性质可得S矩APOM=S矩ONDH=-m，S矩PCNO=S矩MOGB=n，
得S矩APGB=S矩PCDH，
设
则
，
得
，
解得
，
可得S矩APGB=n-m=4①，
S矩PCNO=2S矩APOM即②，
联立①②，解得
，
故答案为：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于E，若AC＝6，BC＝8．
（1）求DE的长；
（2）求△ADB的面积．
-
科目： 来源： 题型：
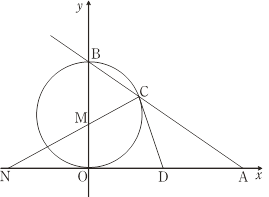
查看答案和解析>>【题目】如图，已知直线AB与x轴、y轴分别交于点A和点B，OA=4，且OA，OB长是关于x的方程x2﹣mx+12=0的两实根，以OB为直径的⊙M与AB交于C，连接CM，交x轴于点N，点D为OA的中点．
（1）求证：CD是⊙M的切线； （2）求线段ON的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将矩形ABCO放在直角坐标系中，其中顶点B的坐标为(10， 8)，E是BC边上一点将△ABE沿AE折叠，点B刚好与OC边上点D重合，过点E的反比例函数y=
的图象与边AB交于点F, 则线段AF的长为( )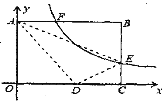 
A.
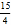B. 2 C. 
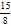D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲袋里装有红球5个，白球2个和黑球12个，乙袋里装有红球20个，白球20个和黑球10个．
（1）如果你想取出1个黑球，选哪个袋子成功的机会大？请说明理由．
（2）某同学说“从乙袋取出10个红球后，乙袋中的红球个数仍比甲袋中红球个数多，所以此时想取出1个红球，选乙袋成功的机会大．”你认为此说法正确吗？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】从共享单车，共享汽车等共享出行到共享雨伞等共享物品，各式各样的共享经济模式在各个领域迅速的普及．
(1) 为获得东台市市民参与共享经济的活动信息，下列调查方式中比较合理的是 ；
A．对某学校的全体同学进行问卷调查
B．对某小区的住户进行问卷调查
C．在全市里的不同社区，选取部分市民进行问卷调查
(2) 调查小组随机调查了东台市民骑共享单车情况，某社区年龄在12～36岁的人有1000人，从中随机抽取了100人，统计了他们骑共享单车的人数，并绘制了如下不完整的统计图表．
骑共享单车的人数统计表
年龄段(岁)
频数
频率
12≤x＜16
2
0.02
16≤x＜20
3
0.03
20≤x＜24
15
a
24≤x＜28
25
0.25
28≤x＜32
b
0.30
32≤x＜36
25
0.25
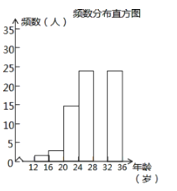
根据以上信息解答下列问题：
① 求出统计表中的a、b，并补全频数分布直方图；
② 试估计这个社区年龄在20岁到32岁(含20岁，不含32岁)骑共享单车的人有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两城市之间开通了动车组高速列车。已知每隔2h有一列速度相同的动车组列车从甲城开往乙城。如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象。请根据图中的信息，解答下列问题：
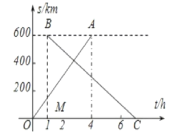
(1)从图象看,普通快车发车时间比第一列动车组列车发车时间___1h(填“早”或“晚”)，点B的纵坐标600的实际意义是___；
(2)请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象；
(3)若普通快车的速度为100km/h，
①求BC的表达式，并写出自变量的取值范围；
②第二列动车组列车出发多长时间后与普通快车相遇?
③请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔.
相关试题
