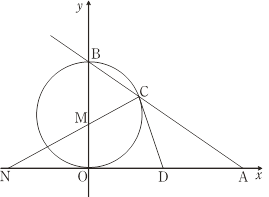
【题目】如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2﹣mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM,交x轴于点N,点D为OA的中点.
(1)求证:CD是⊙M的切线; (2)求线段ON的长.
参考答案:
【答案】(1)证明见解析;(2) NO=![]() .
.
【解析】试题分析:(1)由OA、OB长是关于x的方程x2﹣mx+12=0的两实根,OA=4,则OA×OB=12,根据根与系数的关系可得OB=3,即可得⊙M的半径为1.5;因BM=CM=1.5,根据等腰三角形的性质可得∠OBA=∠BCM;连结OC,OB是⊙M的直径,则∠ACO=90°,D为OA的中点,根据直角三角形斜边的中线等于斜边的一半,可得OD=AD=CD=2, 根据等腰三角形的性质可得∠OAC=∠ACD,又因∠OAC+∠OBA=90°,即可得∠BCM+∠ACD=90°,由此即可判定CD是⊙M的切线.(2)先判断△NOM∽△NCD,根据相似三角形的性质求解即可.
试题解析:
(1)OA、OB长是关于x的方程x2﹣mx+12=0的两实根,OA=4,则OA×OB=12,
得OB=3,⊙M的半径为1.5;
∵BM=CM=1.5,
∴∠OBA=∠BCM.
连结OC,OB是⊙M的直径,则∠ACO=90°,D为OA的中点,
∴OD=AD=CD=2,
∴∠OAC=∠ACD,
又∵∠OAC+∠OBA=90°,
∴∠BCM+∠ACD=90°,
∴∠NCD=90°,
∴CD是⊙M的切线.
(2)∵∠CND=∠CND,∠NOM=∠NCD=90°,
∴△NOM∽△NCD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴NO=![]() .
.
-
科目: 来源: 题型:
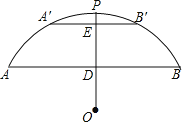
查看答案和解析>>【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,正比例函数y=ax的图象与反比例函数y=
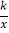 的图象交于点A(3,2)
的图象交于点A(3,2)(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8.
(1)求DE的长;
(2)求△ADB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10, 8),E是BC边上一点将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=
 的图象与边AB交于点F, 则线段AF的长为( )
的图象与边AB交于点F, 则线段AF的长为( ) 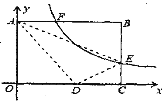
A.
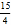 B. 2 C.
B. 2 C. 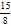 D.
D. 
-
科目: 来源: 题型:
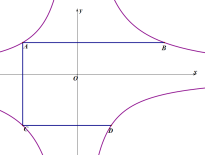
查看答案和解析>>【题目】如图,A、D在反比例函数
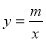
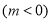 的图像上,点B、C在反比例函数
的图像上,点B、C在反比例函数 的图像上,若AB∥CD∥
的图像上,若AB∥CD∥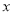 轴,
轴,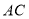 ∥
∥ 轴,且
轴,且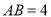 ,
,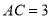 ,
,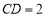 ,则
,则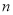 =______.
=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲袋里装有红球5个,白球2个和黑球12个,乙袋里装有红球20个,白球20个和黑球10个.
(1)如果你想取出1个黑球,选哪个袋子成功的机会大?请说明理由.
(2)某同学说“从乙袋取出10个红球后,乙袋中的红球个数仍比甲袋中红球个数多,所以此时想取出1个红球,选乙袋成功的机会大.”你认为此说法正确吗?为什么?
相关试题

