【题目】如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
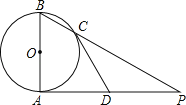
(1)若AB=2,∠P=30°,求AP的长;
(2)若D为AP的中点,求证:直线CD是⊙O的切线.
参考答案:
【答案】(1)AP=2![]() ;(2)见解析
;(2)见解析
【解析】
试题分析:(1)首先根据切线的性质判定∠BAP=90°;然后在直角三角形ABP中利用三角函数的定义求得AP的长度;
(2)连接OC,OD、AC构建全等三角形△OAD≌△OCD,然后利用全等三角形的对应角相等推知∠OAD=∠OCD=90°,即OC⊥CD.
(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,
∴∠BAP=90°;
又∵AB=2,∠P=30°,
∴AP=![]() =
=![]() =2
=2![]() ,即AP=2
,即AP=2![]() ;
;
(2)证明:如图,连接OC,OD、AC.
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),
∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD(直角三角形斜边上的中线等于斜边的一半);
在△OAD和△OCD中,
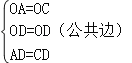 ,
,
∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD(全等三角形的对应角相等);
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,即直线CD是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
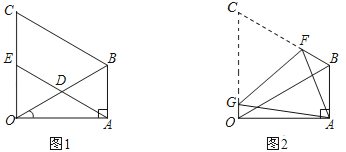
(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是江津区某一天的气温随时间变化的图象,根据图象回答:在这一天中:

(1)气温T(℃)是不是时间t(时)的函数。
(2)12时的气温是多少?
(3)什么时候气温最高,最高时多少?什么时候气温最低,最低时多少?
(4)什么时候气温是气温是4℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】请利用合适的方法进行计算:
(1)(-56)+(+7)+150+(+93)+(-44);
(2)(-12)×(-
 +
+ -
-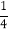 +
+ );
);(3)(-5)×(+
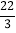 )+(+7)×(-
)+(+7)×(-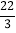 )+12×
)+12×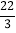 .
.(4)
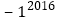 -[(-3)×(2÷3)2-
-[(-3)×(2÷3)2- ÷(-2)2];
÷(-2)2]; -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正数的平方根是2a﹣1和﹣a+2,则这个正数是( )
A. 1 B. 3 C. 4 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】据《云南省生物物种名录(2016版)的》介绍,在素有“动植物王国”之美称的云南,已经发现的动植物有25434种,25434用科学记数法表示为( )
A.2.5434×103 B.2.5434×104 C.2.5434×10﹣3 D.2.5434×10﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点M(﹣2,3)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
相关试题

