【题目】如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
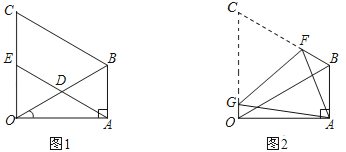
(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
参考答案:
【答案】(1)证明见解析;(2)1.
【解析】
试题分析:(1)首先根据直角三角形中斜边上的中线等于斜边的一半可得DO=DA,再根据等边对等角可得∠DAO=∠DOA=30°,进而算出∠AEO=60°,再证明BC∥AE,CO∥AB,进而证出四边形ABCE是平行四边形;
(2)设OG=x,由折叠可得:AG=GC=8-x,再利用三角函数可计算出AO,再利用勾股定理计算出OG的长即可.
试题解析:(1)∵Rt△OAB中,D为OB的中点,
∴AD=![]() OB,OD=BD=
OB,OD=BD=![]() OB
OB
∴DO=DA,
∴∠DAO=∠DOA=30°,∠EOA=90°,
∴∠AEO=60°,
又∵△OBC为等边三角形,
∴∠BCO=∠AEO=60°,
∴BC∥AE,
∵∠BAO=∠COA=90°,
∴CO∥AB,
∴四边形ABCE是平行四边形;
(2)设OG=x,由折叠可得:AG=GC=8-x,
在Rt△ABO中,
∵∠OAB=90°,∠AOB=30°,BO=8,
∴AO=BOcos30°=8×![]() =4
=4![]() ,
,
在Rt△OAG中,OG2+OA2=AG2,
x2+(4![]() )2=(8-x)2,
)2=(8-x)2,
解得:x=1,
∴OG=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有长为3,5,7,9的四根木条,要选其中的三根组成三角形,选法一共有( )
A. 2种. B. 3种 C. 4种 D. 5种
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形的正投影可能是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若平面直角坐标系内的点M在第四象限,且M到x轴的距离为1,到y轴的距离为2,则点M的坐标为( )
A. (2,1) B. (﹣2,1) C. (2,﹣1) D. (1,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是江津区某一天的气温随时间变化的图象,根据图象回答:在这一天中:

(1)气温T(℃)是不是时间t(时)的函数。
(2)12时的气温是多少?
(3)什么时候气温最高,最高时多少?什么时候气温最低,最低时多少?
(4)什么时候气温是气温是4℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】请利用合适的方法进行计算:
(1)(-56)+(+7)+150+(+93)+(-44);
(2)(-12)×(-
 +
+ -
-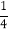 +
+ );
);(3)(-5)×(+
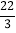 )+(+7)×(-
)+(+7)×(-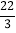 )+12×
)+12×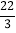 .
.(4)
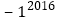 -[(-3)×(2÷3)2-
-[(-3)×(2÷3)2- ÷(-2)2];
÷(-2)2]; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
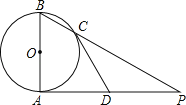
(1)若AB=2,∠P=30°,求AP的长;
(2)若D为AP的中点,求证:直线CD是⊙O的切线.
相关试题

