【题目】“化归与转化的思想”是指在研究解决数学问题时采用某种手段将问题通过变换使之转化,进而使问题得到解决。
(1)我们知道![]() 可以得到
可以得到![]() 。如果
。如果![]() ,求
,求![]() 、
、![]() 的值.
的值.
(2)已知![]()
![]()
![]() 试问多项式a2+b2+c2﹣ab﹣ac﹣bc的值是否与变量
试问多项式a2+b2+c2﹣ab﹣ac﹣bc的值是否与变量![]() 的取值有关?若有关请说明理由;若无关请求出多项式的值.
的取值有关?若有关请说明理由;若无关请求出多项式的值.
参考答案:
【答案】(1)a=-1,b=2 (2)无关 3
【解析】
(1)根据题意,可以将题目中的式子化为材料中的形式,从而可以得到a、b的值;
(2)根据 a2+b2+c2-ab-ac-bc=![]() ,代入求值.
,代入求值.
(1)由a2+b2+2a-4b+5=0,得到:(a2+2a+1)+(b2-4b+4)=0,
(a+1)2+(b-2)2=0,
所以有a+1=0,b-2=0,
解得a=-1,b=2;
(2)多项式 a2+b2+c2-ab-ac-bc的值与变量x的取值无关.理由如下:
∵a=![]() x+2017,b=
x+2017,b=![]() x+2015,c=
x+2015,c=![]() x+2016,
x+2016,
∴a-b=2,a-c=1,c-b=1,
∴a2+b2+c2-ab-ac-bc
=(![]() -ab+
-ab+![]() )+(
)+(![]() -ac+
-ac+![]() )+(
)+(![]() -cb+
-cb+![]() )
)
=![]()
=![]()
=3.
∴多项式 a2+b2+c2-ab-ac-bc的值与变量x的取值无关,且a2+b2+c2-ab-ac-bc的值是3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2mx+m2-1=0.
(1)不解方程,判别方程的根的情况;
(2)若方程有一个根为3,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象与
的图象与  轴交于A、B两点(A在B的左侧),与
轴交于A、B两点(A在B的左侧),与  轴交于点C,顶点为D.
轴交于点C,顶点为D.
(1)求点A、B的坐标,并在下面直角坐标系中画出该二次函数的大致图象;
(2)设一次函数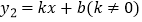 的图象经过B、D两点,请直接写出满足
的图象经过B、D两点,请直接写出满足  的
的  的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,点
,点 为平面内一点,连接
为平面内一点,连接 .
.(1)探究:
如图1:
 ,
, ,则
,则 的度数是___________;
的度数是___________;如图2:
 ,
, ,则
,则 的度数是___________.
的度数是___________.(2)在图2中试探究
 ,
,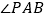 ,
, 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.(3)拓展探究:当点
 在直线
在直线 ,
, 外,如图3、4所示的位置时,请分别直接写出
外,如图3、4所示的位置时,请分别直接写出 ,
,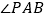 ,
, 之间的数量关系.
之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,是一个长为
 ,宽为
,宽为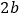 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。(1)你认为图2中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法求图2中阴影部分的面积.
方法1 ;方法2 ;
(3)仔细观察图2,写出
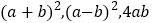 三个代数式之间的等量关系.
三个代数式之间的等量关系.(4)若
 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于雾霾天气对人们健康的影响,市场上的空气净化器成了热销产品.某公司经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=-2x+1000.
(1)该公司每月的利润为w元,写出利润w与销售单价x的函数关系式;
(2)若要使每月的利润为40000元,销售单价应定为多少元?
(3)公司要求销售单价不低于250元,也不高于400元,求该公司每月的最高利润和最低利润分别为多少? -
科目: 来源: 题型:
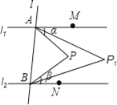
查看答案和解析>>【题目】如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
(1)当点P在l1与l2之间时.
①求∠APB的大小(用含α、β的代数式表示);
②若∠PAM的平分线与∠PBN的平分线交于点P1,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,则∠AP1B= ,∠APnB= .(用含α、β的代数式表示,其中n为正整数)
(2)当点P不在l1与l2之间时.
若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
相关试题

