【题目】如图1,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(-3,4).
(1)求AO的长;
(2)求直线AC的解析式和点M的坐标;
(3)如图2,点P从点A出发,以每秒2个单位的速度沿折线A-B-C运动,到达点C终止.设点P的运动时间为t秒,△PMB的面积为S.
①求S与t的函数关系式;
②求S的最大值.


图1 图2
参考答案:
【答案】(1)5;(2)y=-![]() x+
x+![]() ,M(0,
,M(0,![]() );(3)①S=
);(3)①S= ;②
;②![]() .
.
【解析】
(1)根据A的坐标求出AH、OH,根据勾股定理求出即可;
(2)根据菱形性质求出B、C的坐标,设直线AC的解析式是y=kx+b,把A(-3,4),C(5,0)代入得到方程组,求出即可;
(3)①过M作MN⊥BC于N,根据角平分线性质求出MN,P在AB上,根据三角形面积公式求出即可;P在BC上,根据三角形面积公式求出即可;②求出P在AB的最大值和P在BC上的最大值比较即可得到答案.
(1)∵A(-3,4),
∴AH=3,OH=4,
由勾股定理得:AO=![]() =5;
=5;
(2)∵四边形OABC是菱形,
∴OA=OC=BC=AB=5,
5-3=2,
∴B(2,4),C(5,0),
设直线AC的解析式是y=kx+b,
把A(-3,4),C(5,0)代入得:![]() ,
,
解得: ,
,
∴直线AC的解析式为y=-![]() x+
x+![]() ,
,
当x=0时,y=2.5,
∴M(0,2.5);
(3)①过M作MN⊥BC于N,
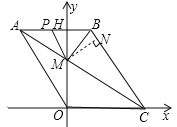
∵四边形OABC是菱形,
∴∠BCA=∠OCA,
∵MO⊥CO,MN⊥BC,
∴OM=MN,
当0≤t<2.5时,P在AB上,MH=4-2.5=![]() ,
,
=![]() ×BP×MH=
×BP×MH=![]() ×(5-2t)×
×(5-2t)×![]() =-
=-![]() t+
t+![]() ,
,
∴S=![]() t+
t+![]() ,
,
当t=2.5时,P与B重合,△PMB不存在;
当2.5<t≤5时,P在BC上,S=![]() ×PB×MN=
×PB×MN=![]() ×(2t-5)×
×(2t-5)×![]() =
=![]() t-
t-![]() ,
,
∴S=![]() t
t![]() ,
,
故S=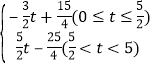 ;
;
②当P在AB上时,高MH一定,只有BP取最大值即可,即P与A重合,S最大是![]() ×5×
×5×![]() =
=![]() ,
,
同理在BC上时,P与C重合时,S最大是![]() ×5×
×5×![]() =
=![]() ,
,
∴S的最大值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三个天平的托盘中形状相同的物体质量相等.图①、图②所示的两个天平处于平衡状态,要使第三个天平也保持平衡,可在它的右盘中放置( )

A. 3个球 B. 4个球
C. 5个球 D. 6个球
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(s,t)(s≠0).
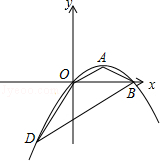
(1)当s=2时,t=1时,求抛物线对应的二次函数的表达式;
(2)若(1)中的抛物线与x轴交于点B,过B作OA的平行线交抛物线于点D,求△BDO三条高的和;
(3)当点A在抛物线y=x2﹣x上,且﹣1≤s<2时,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:

(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,则下列结论中不正确的是( )
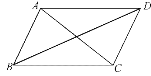
A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】全球变暖,气候开始恶化,中国政府为了对全球气候变暖负责,积极推进节能减排,居民购买节能灯,国家补贴50%购灯费.某县推广财政补贴节能灯后,李阿姨买了4个8W和3个24W的节能灯,一共用了29元;王叔叔买了2个8W和2个24W的节能灯,一共用了17元.该县财政补贴50%后,一个8W、24W节能灯的价格各是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)计算:(﹣1)2017+2cos45°﹣
(2)化简: ÷(1﹣
÷(1﹣  ).
).
相关试题

