【题目】已知,抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(s,t)(s≠0). 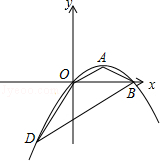
(1)当s=2时,t=1时,求抛物线对应的二次函数的表达式;
(2)若(1)中的抛物线与x轴交于点B,过B作OA的平行线交抛物线于点D,求△BDO三条高的和;
(3)当点A在抛物线y=x2﹣x上,且﹣1≤s<2时,求a的取值范围.
参考答案:
【答案】
(1)解:由题意可知A(2,1),
设抛物线的解析式为y=a(x﹣2)2+1,
由于抛物线过原点,
∴将(0,0)代入y=a(x﹣2)2+1,
∴解得a=﹣ ![]() ,
,
∴抛物线的解析式为:y=﹣ ![]() (x﹣2)2+1
(x﹣2)2+1
(2)解:令y=0代入y=﹣ ![]() (x﹣2)2+1,
(x﹣2)2+1,
∴解得x=4或x=0,
∴B(4,0)
设直线OA的解析式为:y=kx,
将A(2,1)代入y=kx,
∴k= ![]() ,
,
∵BD∥OA,
∴设直线BD的解析式为:y= ![]() x+m,
x+m,
将B(4,0)代入y= ![]() x+m,
x+m,
∴m=﹣2
∴直线BD的解析式为:y= ![]() x﹣2
x﹣2
联立 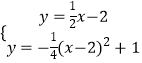
解得:x=4或x=﹣2
∴D(﹣2,﹣3)
∴由勾股定理可知:OD= ![]() ,BD=3
,BD=3 ![]() ,
,
设OB、OD、BD边上的高分别为h1,h2,h3,
∴h1=3
又∵OB=4,
∴S△BDO= ![]() OBh1=6,
OBh1=6,
∴ ![]() BDh3=
BDh3= ![]() ODh2=6,
ODh2=6,
∴h2= ![]() ,h3=
,h3= ![]() ,
,
∴△BDO三条高的和h1+h2+h3=3+ ![]() +
+ ![]()
(3)解:由题意可知:t=s2﹣s,
∵A(s,t)是y=ax2+bx+c(a≠0)的顶点,
∴y=a(x﹣s)2+t,
又因为该抛物线经过原点,
∴0=as2+t,
∴0=as2+s2﹣s,
∴s=(a+1)s2,
当s=0时,
此时,a全体实数,
当s≠0时,此时﹣1≤s<0或0<s<2,
∴a= ![]() ,
,
∴a≤﹣2或a>﹣ ![]() ,
,
综上所述,a≤﹣2或a>﹣ ![]()
【解析】(1)由题意可知A(2,1),设抛物线的解析式为y=a(x﹣2)2+1,由于抛物线过原点,所以将(0,0)代入即可求出a的值.(2)根据A(2,1)可求出OA的直线解析式,由于DB∥OA,所以一次项系数必定相等,从而可求出直线BD的解析式,联立直线BD与抛物线的解析式即可求出D的坐标,然后根据勾股定理分别求出OD、BD的长度,再求出BOD的面积即可求出△BDO三条高的和.(3)t=s2﹣s,由于A(s,t)是y=ax2+bx+c(a≠0)的顶点,所以y=a(x﹣s)2+t,将(0,0)代入该式后可得s=(a+1)s2 , 利用s的范围即可求出a的范围.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲跑步中途改为步行,到达图书馆恰好用30 min.小东骑自行车以300 m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图9所示.
(1)家与图书馆之间的路程为 m,小玲步行的速度为 m/min;
(2)求小东离家的路程y关于x的函数解析式,并写出自变量的取值范围;
(3)求两人相遇的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三个天平的托盘中形状相同的物体质量相等.图①、图②所示的两个天平处于平衡状态,要使第三个天平也保持平衡,可在它的右盘中放置( )

A. 3个球 B. 4个球
C. 5个球 D. 6个球
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:

(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(-3,4).
(1)求AO的长;
(2)求直线AC的解析式和点M的坐标;
(3)如图2,点P从点A出发,以每秒2个单位的速度沿折线A-B-C运动,到达点C终止.设点P的运动时间为t秒,△PMB的面积为S.
①求S与t的函数关系式;
②求S的最大值.


图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,则下列结论中不正确的是( )
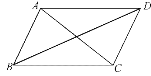
A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
相关试题

