搜索
【题目】如图，□ABCD纸片，∠A=120°，AB=4，BC=5，剪掉两个角后，得到六边形AEFCGH ,它的每个内角都是120°，且EF=1，HG=2，则这个六边形的周长为( )
A. 12 B. 15 C. 16 D. 18
参考答案：
【答案】B
【解析】如图，分别作直线AB、BC、HG的延长线和反向延长线使它们交于点B、Q、P.
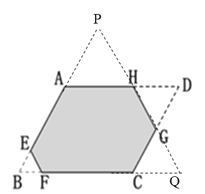
∵六边形ABCDEF的六个角都是120°，
∴六边形ABCDEF的每一个外角的度数都是60°.
∴△APH、△BEF、△DHG、△CQG都是等边三角形。
∴EF=BE=BF=1，DG=HG=HD=2.
∴FC=5-1=4，AH=5-2= 3，CG=CD-DG=42=2.
∴六边形的周长为1+3+3+2+2+4=15.
故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：(-s)7÷(-s)5 =____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】温度通常有两种表示方法：华氏度（单位：℉）与摄氏度（单位：℃），已知华氏度数y与摄氏度数x之间是一次函数关系，如表列出了部分华氏度与摄氏度之间的对应关系：
摄氏度数x（℃）
…
0
…
35
…
100
…
华氏度数y（℉）
…
32
…
95
…
212
…
（1）选用表格中给出的数据，求y关于x的函数解析式（不需要写出该函数的定义域）；
（2）已知某天的最低气温是﹣5℃，求与之对应的华氏度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，Rt△ABC中，∠ACB=Rt∠，AC=8，BC=6，点D为AB的中点，动点P从点A出发，沿AC方向以每秒1个单位的速度向终点C运动，同时动点Q从点C出发，以每秒2个单位的速度先沿CB方向运动到点B，再沿BA方向向终点A运动，以DP，DQ为邻边构造PEQD，设点P运动的时间为t秒．
（1）当t=2时，求PD的长；
（2）如图2，当点Q运动至点B时，连结DE，求证：DE∥AP.
（3）如图3，连结CD．
①当点E恰好落在△ACD的边上时，求所有满足要求的t值；
②记运动过程中PEQD的面积为S，PEQD与△ACD的重叠部分面积为S1，当
＜
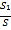时，请直接写出t的取值范围是 ______ ．
-
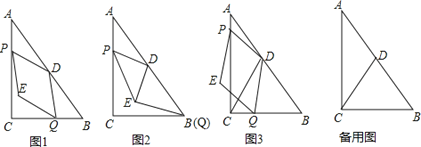
科目： 来源： 题型：
查看答案和解析>>【题目】（满分8分）如图，某教学楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，教学楼在建筑物的墙上留下高2m的影子CE；而当光线与地面的夹角是45°时，教学楼顶A在地面上的影子F与墙角C的距离为18m (B、F、C在一条直线上).
求教学楼AB的高度.（结果保留整数）
（参考数据：sin22°
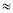0.37，cos22°
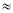0.93，tan22°
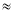0.40 .）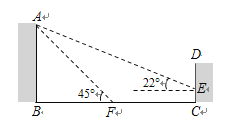
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在△ABC中，M、N分别是边AB、AC的中点，D是边BC延长线上的一点，且CD=
BC，联结CM、DN． 求证：四边形MCDN是平行四边形．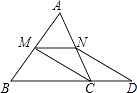
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中正确的是（ ）
A.延长射线OA到点B
B.线段AB为直线AB的一部分
C.射线OM与射线MO表示同一条射线
D.一条直线由两条射线组成
相关试题
