【题目】如图,动点A,B从原点O同时出发,点A以每秒a个单位长度向x轴的负半轴向左运动,点B以每秒b个单位长度沿y轴的正半轴向上运动. 
(1)若a,b满足关系|a+b﹣3|+(a﹣ ![]() b)2=0,请求出a,b的值;
b)2=0,请求出a,b的值;
(2)如图①,求当运动时间为2秒时,直线AB的函数表达式; 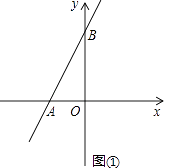
(3)如图②,∠BAO与∠ABO的外角平分线相交于点C,随着点A,点B的运动,∠C的度数是否会发生变化?若度数变化,请说明理由;若度数不变,请求出∠C的度数. 
参考答案:
【答案】
(1)解:根据题意可得:  ,
,
解得: ![]()
(2)解:由(1)知,当运动时间为2秒时,点A坐标为(﹣2,0),点B坐标为(0,4),
设直线AB解析式为y=mx+n,
将A(﹣2,0)、B(0,4)代入,得: ![]() ,
,
解得: ![]() ,
,
∴直线AB的解析式为y=2x+4
(3)解:随着点A,点B的运动,∠C的度数不会发生变化,
∵∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠BAO与∠ABO的外角和为180°﹣∠OAB+180°﹣∠ABO=360°﹣(∠OAB+∠OBA)=270°,
∵AC、BC分别平分这两个外角,
∴∠CAB+∠CBA=135°,
∴∠C=45°
【解析】(1)根据非负数的性质可得关于a、b的方程组,求解可得;(2)由(1)中a、b的值可得点A、B的坐标,再用待定系数法即可求得解析式;(3)先求出△ABO两个外角度数为270°,再根据角平分线可得△ABC两个内角度数,从而可得∠C.
【考点精析】解答此题的关键在于理解解二元一次方程组的相关知识,掌握二元一次方程组:①代入消元法;②加减消元法,以及对确定一次函数的表达式的理解,了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
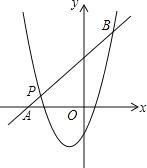
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )

A. 3
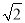 km B. 3
km B. 3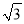 km C. 4km D. (3
km C. 4km D. (3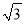 -3)km
-3)km -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表(满分100分)
分数段/分
61~70
71~80
81~90
91~100
人数/人
2
8
6
4
若已知成绩在91-100分的同学为优胜者.那么优胜率为%。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m2﹣3m﹣1=0,则3m2﹣9m+2016的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,1)与点A′(5,b)是关于原点对称,则a= , b= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣ ax4y3)
ax4y3) 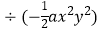 2y﹣1
2y﹣1
(2)(x﹣2)(x+2)﹣(x+1)(x﹣3)+(﹣3)0
(3)(2x﹣1)(﹣1﹣2x)+(2x+1)2﹣2.
相关试题

