【题目】下列各式从左到右的变形中,为因式分解的是( )
A.x(a﹣b)=ax﹣bx
B.x2﹣1+y2=(x﹣1)(x+1)+y2
C.y2﹣1=(y+1)(y﹣1)
D.ax+by+c=x(a+b)+c
参考答案:
【答案】C
【解析】解:A、是整式的乘法,故A错误;
B、没把一个多项式转化成几个整式积,故B错误;
C、把一个多项式转化成几个整式积,故C正确;
D、没把一个多项式转化成几个整式积,故D错误;
故选:C.
【考点精析】利用因式分解的定义对题目进行判断即可得到答案,需要熟知因式分解的最后结果必须是几个整式的乘积,否则不是因式分解;因式分解的结果必须进行到每个因式在有理数范围内不能再分解为止.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x2+x3=x5
B.x8÷x2=x4
C.3x﹣2x=1
D.(x2)3=x6 -
科目: 来源: 题型:
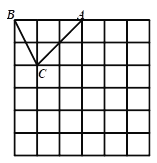
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
-
科目: 来源: 题型:
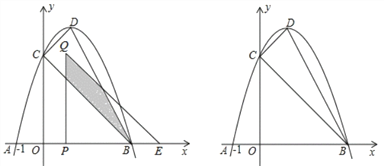
查看答案和解析>>【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 如果两条直线被第三条直线所截,那么同位角相等;
B. 点到直线的距离是指直线外一点到这条直线的垂线段的长度;
C. 同旁内角相等,两直线平行;
D. 经过一点有且只有一条直线与已知直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索与研究:
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?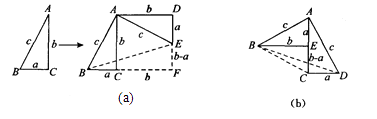
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=3x+6中,y的值随x的增大而 .
相关试题

