【题目】数列:0,2,4,8,12,18,…是我国的大衍数列,也是世界数学史上第一道数列题.该数列中的奇数项可表示为![]() ,偶数项表示为
,偶数项表示为![]() .
.
如:第一个数为![]() =0,第二个数为
=0,第二个数为![]() =2,…
=2,…
现在数轴的原点上有一点P,依次以大衍数列中的数为距离向左右来回跳跃.
第1秒时,点P在原点,记为P1;
第2秒时,点P向左跳2个单位,记为P2,此时点P2所表示的数为-2;
第3秒时,点P向右跳4个单位,记为P3,此时点P3所表示的数为2;
…
按此规律跳跃,点P20表示的数为______.
参考答案:
【答案】-110
【解析】
通过总结规律和数轴上表示即可求解.
第1秒时,点P在原点,记为P1;
第2秒时,点P向左跳2个单位,记为P2,此时点P2所表示的数为-2;
第3秒时,点P向右跳4个单位,记为P3,此时点P3所表示的数为2;
第4秒时,点P向左跳8个单位,记为P4,此时点P3所表示的数为-6;
第5秒时,点P向右跳12个单位,记为P5,此时点P4所表示的数为6;
第6秒时,点P向左跳18个单位,记为P6,此时点P5所表示的数为-12;
第7秒时,点P向右跳24个单位,记为P7,此时点P6所表示的数为12;

通过规律得出以0为轴左右两边的绝对值相等,符号相反,只要求出一边即可得出结论,通过秒数为奇数 1对应0,3对应2,5对应6,7对应12,以此推类得出奇数所对应的数值为![]() ,将P21代入得110,所以P20为-110.
,将P21代入得110,所以P20为-110.
答案为-110.
-
科目: 来源: 题型:
查看答案和解析>>【题目】①在数轴上没有点能表示
 +1;②无理数是开不尽方的数;③存在最小的实数;④4的平方根是±2,用式子表示是
+1;②无理数是开不尽方的数;③存在最小的实数;④4的平方根是±2,用式子表示是 =±2;⑤某数的绝对值,相反数,算术平方根都是它本身,则这个数是0,其中正确的是______.
=±2;⑤某数的绝对值,相反数,算术平方根都是它本身,则这个数是0,其中正确的是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】元旦晚会上,王老师要为她的学生及班级的六位科任老师送上贺年卡,网上购买贺年卡的优惠条件是:购买50或50张以上享受团购价.王老师发现:零售价与团购价的比是5:4,王老师计算了一下,按计划购买贺年卡只能享受零售价,如果比原计划多购买6张贺年卡就能享受团购价,这样她正好花了100元,而且比原计划还节约10元钱;
(1)贺年卡的零售价是多少?
(2)班里有多少学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.C点的坐标是 , △ABC的面积为 .
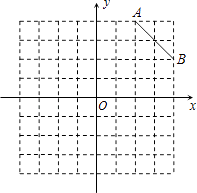
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为 .
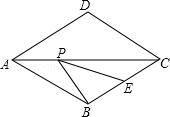
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆的半径为
 个单位长度.数轴上每个数字之间的距离为1个单位长度,在圆的4等分点处分别标上点A,B,C,D.先让圆周上的点A与数轴上表示-1的点重合.
个单位长度.数轴上每个数字之间的距离为1个单位长度,在圆的4等分点处分别标上点A,B,C,D.先让圆周上的点A与数轴上表示-1的点重合.(1)圆的周长为多少?
(2)若该圆在数轴上向右滚动2周后,则与点A重合的点表示的数为多少?
(3)若将数轴按照顺时针方向绕在该圆上,(如数轴上表示-2的点与点B重合,数轴上表示-3的点与点C重合…),那么数轴上表示-2018的点与圆周上哪个点重合?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.

(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
相关试题

