【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B 运动.设 动点P的运动时间为t秒
(1)当t为何值时,四边形PODB是平行四边形?
(2)在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由。
(3) 在线段PB上有一点M,且PM=5,当P运动 秒时,四边形OAMP的周长最小, 并画图标出点M的位置。


参考答案:
【答案】(1)t=2.5;(2)t=4 Q(3,4);t=1 Q(-3,4)(3)t=![]()
【解析】(1)根据平行四边形的性质就可以知道PB=5,可以求出PC=5,从而可以求出t的值;(2)要使ODQP为菱形,可以得出PO=5,由三角形的勾股定理就可以求出CP的值而求出t的值;(3)根据题意即可填得t的值.
解: (1)∵四边形PODB是平行四边形,
∴PB=OD=5,
∴PC=5,
∴2t=5,t=2.5;
(2)当Q点在P的右边时
∵四边形ODQP为菱形,
∴OD=OP=PQ=5,
∴在Rt△OPC中,由勾股定理得:
PC=3,
∴2t=3;t=1.5 Q(8,4).
当Q点在P的左边且在BC线段上时,t=4, Q(3,4);
当Q点在P的左边且在BC的延长线上时,t=1,Q(-3,4) .
(3)t=![]() .
.
“点睛”本题考查了平行四边形的判定及性质,菱形的性质,勾股定理的运用,解题时要运用分类讨论的思想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣1,2)关于x轴对称的点的坐标是( )
A. (﹣1,2) B. (﹣2,1) C. (﹣1,﹣2) D. (1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分))规定a*b=2a×2b
(1)求2*3;
(2)若2*∣x+1∣=16,求x的值.。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 平移不改变图形的形状,旋转使图形的形状发生改变
B. 平移和旋转的共同之处是改变图形的位置和大小
C. 一对对应点与旋转中心的距离相等
D. 由旋转得到的图形也一定可以通过平移得到
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD,AB=
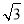 ,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.
,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.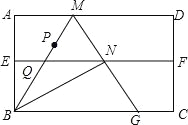
(1)求证:∠ABM=30°;
(2)求证:△BMG是等边三角形;
(3)若P为线段BM上一动点,求PN+PG的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:﹣[﹣(﹣4)]=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+ax﹣1=0的根的情况是( )
A. 没有实数根 B. 只有一个实数根
C. 有两个相等的实数根 D. 有两个不相等的实数根
相关试题

