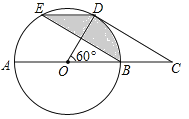
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为![]() 的中点,连接DE,EB.
的中点,连接DE,EB.
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
参考答案:
【答案】(1)证明见试题解析;(2)6.
【解析】
试题分析:(1)先证明DE∥BC,再由CD是⊙O的切线,得到OD⊥CD,于是得到BE∥CD,即可证得结论;
(2)连接OE,由(1)知,![]() ,得到∠BOE=120°,根据扇形的面积公式列方程即可得到结论.
,得到∠BOE=120°,根据扇形的面积公式列方程即可得到结论.
试题解析:(1)∵∠BOD=60°,∴∠AOD=120°,∴![]() ,∵E为
,∵E为![]() 的中点,∴
的中点,∴![]() ,∴DE∥AB,OD⊥BE,即DE∥BC,∵CD是⊙O的切线,∴OD⊥CD,∴BE∥CD,∴四边形BCDE是平行四边形;
,∴DE∥AB,OD⊥BE,即DE∥BC,∵CD是⊙O的切线,∴OD⊥CD,∴BE∥CD,∴四边形BCDE是平行四边形;
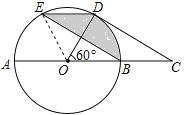
(2)连接OE,由(1)知,![]() ,∴∠BOE=120°,∵阴影部分面积为6π,∴
,∴∠BOE=120°,∵阴影部分面积为6π,∴![]() ,∴r=6.
,∴r=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列命题中,是真命题的是( )
A.两条对角线相等的四边形是矩形
B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相平分的四边形是平行四边形
D.两条对角线互相垂直且相等的四边形是正方形
-
科目: 来源: 题型:
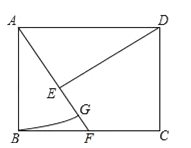
查看答案和解析>>【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A、B两点的距离相等.
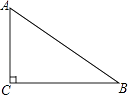
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=32°,求∠CAD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形﹣正八边形.

(1)如图②,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹);
(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于 .
-
科目: 来源: 题型:
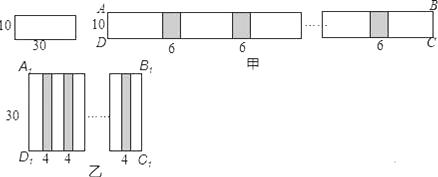
查看答案和解析>>【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形A1B1C1D1,黏合部分的长度为4cm.若长为30cm,宽为10cm的长方形白纸条共有100张,则小明应分配到 张长方形白纸条,才能使小明和小慧按各自要求黏合起来的长方形面积相等(要求100张长方形白纸条全部用完).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只蚂蚁沿直角三角形的边长爬行一周需2秒,如果将直角三角形的边长扩大1倍,那么这只蚂蚁再沿边长爬行一周需 ( ).
(A)6秒 (B)5秒 (C)4秒 (D)3秒
相关试题

