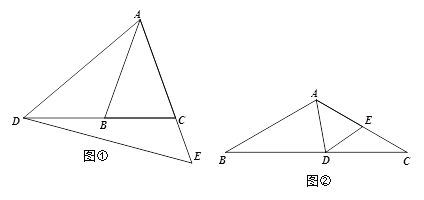
【题目】如图,△ABC中,![]() ,点D在BC所在的直线上,点E在射线AC上,且
,点D在BC所在的直线上,点E在射线AC上,且![]() ,连接DE.
,连接DE.
(1)如图①,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)当点D在直线BC上(不与点B、C重合)运动时,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
参考答案:
【答案】(1)35°(2)30°(3)∠BAD=2∠CDE
【解析】(1).根据∠ACB=∠E+∠CDE=∠E-∠CDE+∠BAD,即可求解;(2).同(1) 的方法可求解;(3).分两种情况讨论:①当点D在点B的左侧时;②当点D在线段BC上时,注意分类讨论的思想.
本题解析:(1)∵∠ACB=∠E+∠CDE, ∠ACB=∠E-∠CDE+∠BAD, ∴∠CDE=35°
(2)![]()
(3)设![]() ,
,![]() ,
,![]() ,
,
![]()
①如图1,当点D在点B的左侧时,![]()
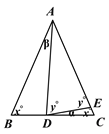
∴![]() ,
,![]() 得,
得,![]() ,∴
,∴![]() `
`
②如图2,当点D在线段BC上时,![]() ,
,
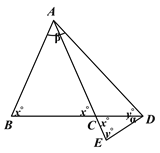
∴![]() ,
,![]() 得,
得,![]() ,∴
,∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础。结合数轴与绝对值的知识回答下列问题:

(1)数轴上表示1和4的两点之间的距离是______;表示-3和2的两点之间的距离是______;
表示数a和-2的两点之间的距离是3,那么a=________;一般地,数轴上表示数a和数b的两点之间的距离等于__________.
(2)若数轴上表示数a的点位于-4与2之间,则
 =_______.
=_______.(3)是否存在数a,使代数式
 的值最小?如果存在,请写出数a=______,此时代数式
的值最小?如果存在,请写出数a=______,此时代数式 的最小值是__________.
的最小值是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣3,0)、B(5,0)、C(0,5)三点,O为坐标原点
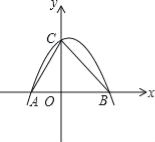
(1)求此抛物线的解析式;
(2)若把抛物线y=ax2+bx+c(a≠0)向下平移
 个单位长度,再向右平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
个单位长度,再向右平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;(3)设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“五一”期间,某公司组织员工到扬州瘦西湖旅游,如果租用甲种客车2辆,乙种客车3辆,则可载180人,如果租用甲种客车3辆,乙种客车1辆,则可载165人.
(1)请问甲、乙两种客车每辆分别能载客多少人?
(2)若该公司有303名员工,旅行社承诺每辆车安排一名导游,导游也需一个座位.
①现打算同时租甲、乙两种客车共8辆,请帮助旅行社设计租车方案.
②旅行前,旅行社的一名导游由于有特殊情况,旅行社只能安排7名导游,为保证所租的每辆车均有一名导游,租车方案调整为:同时租65座、45座和30座的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问旅行社的租车方案如何安排?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. ﹣4x8÷2x4=﹣3x2 B. 2x3x=6x C. ﹣2x+x=﹣3x D. (﹣x3)4=x12
-
科目: 来源: 题型:
查看答案和解析>>【题目】2004×2006-20052= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个两位数的十位上的数字相同,其中一个两位数的个位上的数字是6,另一个两位数的个位上的数字是4,它们的平方差是220,求这两位数..
相关试题

