【题目】如图，AB是⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．

（1）求证：；

（2）若，，求CD的长．

【答案】(1)见解析；（2）.

【解析】

（1）连接OC，根据切线的性质，判断出AD∥OC，再应用平行线的性质，即可推得．

(2)连接BC，通过证明△ADC△ACB，可求出AD的长，再在Rt△ADC中，通过勾股定理可求出CD的长.

解：（1）证明：如图，连接OC，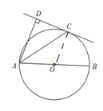
，
∵CD是⊙O的切线，
∴OC⊥CD．
∵AD⊥CD，
∴AD∥OC，
∴∠DAC=∠ACO．
∵OA=OC，
∴∠CAB=∠ACO，
∴∠DAC=∠CAB.
(2)如图，连接BC

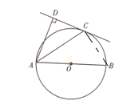
∵AB是⊙O的直径，

∴∠ACB=90°.

∵AD⊥CD，

∴∠ADC=90°.

∴∠ADC=∠ACB.

由（1）知∠DAC=∠CAB，

∴△ADC△ACB.

∴.

∵，,则可设AD=2x,AB=3x,x>0,

∴.

解得x=2.

∴AD=4.

在Rt△ADC中，由勾股定理，得CD==.

关闭